Counting fixed-height tatami tilings
Frank Ruskey,
Department of Computer Science,
University of Victoria, Canada.
Jennifer Woodcock,
Department of Computer Science,
University of Victoria, Canada.
Abstract:
A tatami tiling is an arrangement of 1 by 2 dominoes (or mats) in a rectangle
with m rows and n columns, subject to the constraint
that no four corners meet at a point.
For fixed m we present and use Dean Hickerson's combinatorial
decomposition of the set of tatami tilings --- a decomposition that
allows them to be viewed as certain classes of
restricted compositions when n > m.
Using this decomposition we find the ordinary generating functions of both
unrestricted and inequivalent tatami tilings that fit in a rectangle
with m rows and n columns,
for fixed m and n > m.
This allows us to verify a modified version of a conjecture of Knuth.
Finally, we give explicit solutions for the count of tatami tilings, in
the form of sums of binomial coefficients.
Tatami tilings of height 2, 3, 4
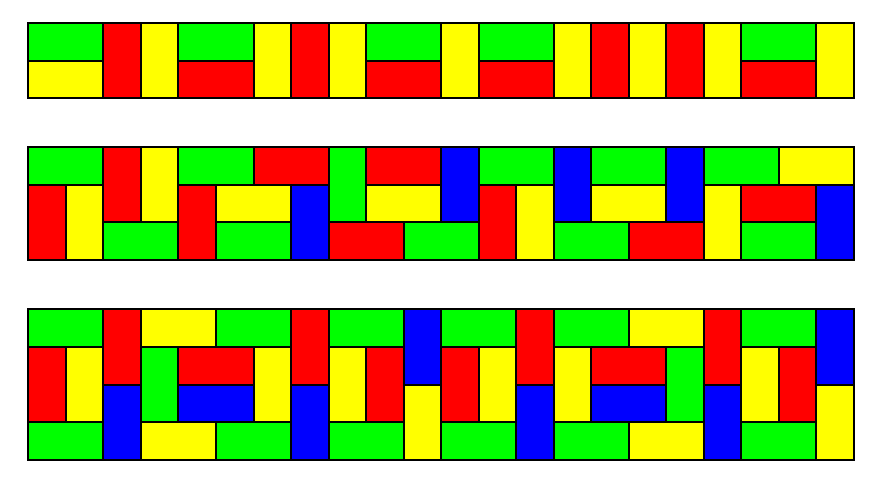
-
Files: pdf.
-
Electronic Journal of Combinatorics, Paper R126 (2009) 20 pages.
-
Accepted August 30, 2009.
-
Please send me a note if
you download one of these files.
It's always nice to know who's reading your papers.
-
Jenni Woodcock gave a talk about this paper at the 36th
ACCMCC conference in Newcastle, Australia, 7-11 December 2009.
Here it is: 33accmcc.pdf.
-
Below are some links to sites about tatami layouts.
Note that the layouts considered in our paper are
"auspicious" layouts.
-
Selected citations:
-
A. Alhazov, K. Morita, and C. Iwamoto,
A Note on Tatami Tilings,
LA Symposium 2009, Kyoto University, February 2010, 6 pages.
[This paper finds a generating function for the case
where both dimensions are odd and there is one monomer.]
-
More recent developments:
Abstract.
Back to list of publications.