COMBINATORIAL ALGORITHMS GROUP Schedule of Talks: Fall 2012

For any surface S, a graph that embeds on a surface S having a maximum number of edges with every face bound by three edges, is known as a triangulation of S. The irreducible triangulations of S are sought to characterize the family of triangulations on S. We will discuss their definition, see examples for low genus surfaces, and present known properties of these graphs for both orientable and nonorientable surfaces.

Wang tiles are sets of squares with colored edges, and laying Wang tiles adjacently produces a valid tiling if adjacent edges always share the same color. Surprisingly, there exists finite tile sets which tile the whole plane but only do so aperiodically (A finite tile set consists of a finite number of different edge colorings, but infinite copies of each tile with a particular coloring). Since their discovery in 1966 an open question has been: what is the smallest tile set that only tiles aperiodically? The first example by Berger had 20,426 tiles, Robinson reduced that number to 56, and the current record-holder is the Cari-Kulic with 13 tiles. In this talk, I will give an outline of Robinson's hierarchical 56 piece tiling set and the quite-different Cari-Kulic 13 piece tiling set.

This year marks the 100th anniversary of the birth of the "father of computer science," Allan Turing. His legacy is recognized with the Turing Award, the "Nobel prize" of computer science. The Department of Computer Science is honoured to host 2010 Turing award winner Leslie Valiant, who has made fundamental contributions to our understanding of computation, communication and learning.

Living organisms function according to protein circuits. Darwin's theory of evolution suggests that these circuits have evolved through variation guided by natural selection. However, the question of which circuits can so evolve in realistic population sizes and within realistic numbers of generations has remained essentially unaddressed.

We suggest that computational learning theory offers the framework for investigating this question, of how circuits can come into being adaptively from experience, without a designer. We formulate evolution as a form of learning from examples. The targets of the learning process are the functions of highest fitness. The examples are the experiences. The learning process is constrained so that the feedback from the experiences is Darwinian. We formulate a notion of evolvability that distinguishes function classes that are evolvable with polynomially bounded resources from those that are not. The dilemma is that if the function class, say for the expression levels of proteins in terms of each other, is too restrictive, then it will not support biology, while if it is too expressive then no evolution algorithm will exist to navigate it. We shall review current work in this area.

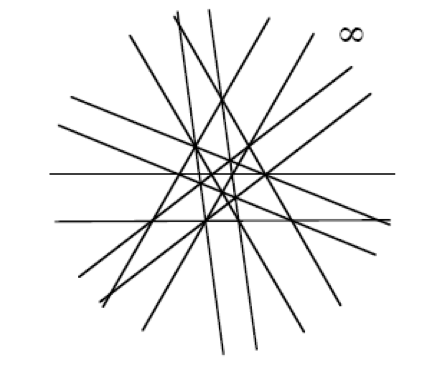
A finite family of (straight) lines in the projective plane is a simplicial arrangement provided all faces (connected components of the complement) are triangles (simplices). Similarly for arrangements of (hyper)planes in higher dimensions. Starting with their first appearance in 1940, simplicial arrangements have attracted attention for their unexpected and unpredictable aspects. While originally investigated due to their extremal properties, more recently connections were found to various algebraic and combinatorial topics. Many open problems remain; most prominent among them is the question whether in all dimensions the number of sporadic (that is unsystematic) arrangements is finite. In particular, in the plane there are three infinite (systematic) families, and there are ninety- four known sporadic ones - but it is still possible that there is an infinite number of these.

A simplicial arrangement of 13 lines, including “line at infinity”

Inverse eigenvalue problems have received considerable attention, and arise frequently in engineering applications. Many inverse eigenvalue problems reduce to the construction of a matrix with prescribed spectral data. One interesting problem is based on the Cauchy interlacing inequalities for symmetric matrices, which asserts that if A is a symmetric matrix of order n and B a principal submatrix of order n-1, then the eigenvalues λ₁, ... , λ_n of A interlace the eigenvalues μ₁, ... , μ_n-1 of B, that is: λ₁ ≤ μ₁ ≤ λ₂ ≤ μ₂ ≤ ... μ_n-1 ≤ λ_n. Duarte has proven that when each of the inequalities is strict, for each tree T on n vertices there exists a real symmetric matrix A whose graph is T such that A has eigenvalues λ₁, ... , λ_n and the principal submatrix obtained from A by deleting its last row and column has eigenvalues μ₁, ... , μ_n-1. In this talk we will show how we can combine some basic analysis (the Implicit Function Theorem), and some basic linear algebra (the structure of the centralizer of a symmetric matrix) to extend Duarte's result to arbitrary connected graphs.

This is joint work with Keivan Hassani Monfared.

A class of cyclic objects on n elements is a class of combinatorial objects on these elements. Isomorphisms of objects in this class are permutations of S_n, and the automorphism group of each object in the class contains a complete cycle of length n. Such classes include circulant graphs, circulant digraphs, cyclic designs and cyclic codes. Brand characterized the set of permutations by which two cyclic combinatorial objects on p^r elements are equivalent for p odd. Using these results, Huffman et al. explicitly gave this set in the case p^2. However, they were unable to provide a generalization to the case p^r, r > 2. We used the classification of doubly to classify the automorphism groups of cyclic codes for any n. We also found extend the results of Brand and Huffman et al. to the case r > 2. We gave algorithms to solve this problem partially.

The chop vector of a set S of celery sticks of positive integer lengths is the infinite vector v_S = (v₁,v₂,v₃,...), where each v_w is the minimum number of cuts needed to chop S into unit pieces, using a knife that can cut up to w sticks at a time. In this talk we see a connection (found jointly with my graduate student Thao Do) between the set of chop vectors and the lattice of integer partitions.

Everyone is welcome to join in for refreshements at the Grad Center after this talk.

In the 1979 Pulitzer Prize winning book "Godel, Escher, Bach: an Eternal Golden Braid", Douglas R. Hofstadter introduced the recurrence relation Q(n)=Q(n-Q(n-1))+Q(n-Q(n-2)) with Q(1)=Q(2)=1. We call this a nested recurrence relation because it has a sub-expression of the form ...Q(...Q(...)...).... Other than composition, the only operations that are used are addition and subtraction.

Some nested recurrence relations have a solution and combinatorial interpretations, while others seemingly do not. For example it is still unknown whether Q(n)is defined for all n. On the other hand, for the closely related recurrence T(n)=T(n-1-T(n-1))+T(n-2-T(n-2)) with T(1)=T(2)=1, the number T(n) counts the maximum number of leaves at the lowest level in a binary tree with n nodes. Some nested recurrence relations are undecidable in the sense that there is no algorithm to decide whether, given a set of initial conditions, they are well-defined for all n > 0. The purpose of this talk is to introduce nested recurrence relations, discuss some of the known results, and present tantalizing open problems.

This is joint work with Marcel Celaya, Steve Tanny, Brad Jackson, Alejandro Erickson and Bram Isgur.

Additional Notes: Cookies and Coffee Provided

A dynamic graph algorithm for maintaining connectivity is a data structure for a graph on a fixed set of n nodes which can process updates in the form of edge insertions and deletions,and answer queries of the form ``Are nodes x and y connected?" This problem has been studied for over 30 years.

In 1983 Fredrickson developed a O(sqrt(m)) worst case time algorithm for this problem. Modified by Eppstein to O(sqrt(n)) in 1993, this data structure remains the only method for the good worst case performance.

In mid 1990's Henzinger and King developed the first data structure with polylogarithmic amortized expected running time, which was improved and made deterministic a few years later by Holm, de Lichtenberg and Thorup. However these data structures can incur a cost of n for a single update.

I'll describe my experiences in this area, how I came to work in the area, and how the ideas for this problem evolved, leading to the recent result of Bruce Kapron, Ben Mountjoy, and myself, a polylogarithmic worst case monte carlo algorithm for this problem which has just won the best paper award in SODA 2013.

Garg, Vazarani, and Yannakakis showed that the integrality gap for (the natural LP relaxation of) maximum disjoint paths (MEDP) in planar graphs is Omega(sqrt(n)). Noting that their gap example (a grid minor) all but disappears if edge congestion 2 is allowed, Kleinberg and Tardos asked if MEDP in planar graphs behaves better when one admits constant congestion. A sequence of results ultimately showed that with constant (in fact 2) congestion, the integrality gap is indeed O(1). (In addition, recent work of Chuzhoy shows a polylog(n) gap in general graphs with constant congestion.) There are strong connections to a parallel stream of work on routing all demands with minimum congestion. This latter work is on "flow-cut gaps" which amounts to embedding a finite metric in L1. We discuss the connections and distinctions between the max throughput and min congestion problems, with an emphasis on highlighting some of the open problems @