|
|
COMBINATORIAL ALGORITHMS GROUP
|
|
If you would like to give a talk in our seminar series, please contact Wendy Myrvold (wendym@cs.uvic.ca). To get e-mail notification of our seminars and other events, you can subscribe to the CAG e-mail list at http://mailman.csc.uvic.ca/mailman/listinfo/cag
| Date | Place | Time | Speaker | Abbreviated Title |
|---|---|---|---|---|
| Tues. Jan. 6 | 1:30pm | ECS 108 | Sylvain Lazard | Computational Geometry and Computer Algebra |
| Fri. Jan. 9 | 2:30pm | ECS 660 | Christophe Weibel | Complexity of Minkowski Sums of Polytopes |
| Fri. Jan. 9 | 2:30pm | ECS 660 | Linqiao Zhang | On the Size of the 3D Visibility Skeleton |
| Fri. Jan. 23 | 2:30pm | DSB C 128 | Branko Grünbaum | Configurations of points and lines: A brief survey |
| Fri. Feb. 13 | 2:30pm | DSB C122 | Frank Ruskey | The hidden mathematical beauty of Venn Diagrams |
| Fri. Feb. 20 | 2:30pm | ECS 660 | Aaron Williams | Shift Gray codes, shorthand universal cycles, and the cool-lex variation of lexicographic order |
| Feb. 21-22 | _ | _ | _ | 11th Coast Combinatorics Conference Feb. 21-22 |
| Fri. Feb. 27 | 2:30pm | Cornett A128 | Amites Sarkar | Partitioning Random Geometric Covers |
| Mon. Mar. 2 | 10:00am | ECS 660 | Ian Munro | Succinct Data Structures |
| Fri. Mar. 6 | 2:30pm | No CAG. | _ | 40th SE Conference |
I will address in this talk some connections between the fields of computational geometry and computer algebra. Typically, computer algebra tools and techniques can be used in geometric algorithms as well as for proving theorems in geometry. Precisely, I will present some work on various constant-complexity geometric problems in three dimensions and, in particular, on lines tangent to four objects, Voronoi diagrams of lines and intersections of quadrics.
Minkowski sum is a basic operation with applications in all kinds of fields. The combinatorial properties of sums of polytopes are however not well known. We present in this talk some recent results and bounds on the number of vertices and facets sums of polytopes can have in function of their summands. In particular, we prove the exact maximal number of faces of a sum of any number of 3-dimensional polytopes.
The 3D visibility skeleton is a data structure that encodes global visibility information of a given scene. While this data structure is very useful in answering global visibility queries, its size typically has high order worst case complexity, and thus is prohibitive to use. Previous theoretical research has indicated that the expected size of this data structure can be linear under some restricted conditions. This talk presents our study on several aspects of the size of the visibility skeleton.
We first show that, through our experimental study of input scenes of polytopes, the actual size of the 3D visibility skeleton is quadratically related to the size of the input and linearly related to the expected silhouette size of the input polytopes. This result is much lower than the worst case complexity, but higher than the expected linear complexity that we had initially hoped for. We suggest theoretical explanations for our obtained experimental results.
We also present a new, succinct 3D visibility skeleton data structure, which potentially reduces the size and computation time of the full 3D visibility skeleton. In addition, this succinct version allows the recovering of the omitted visibility information efficiently.
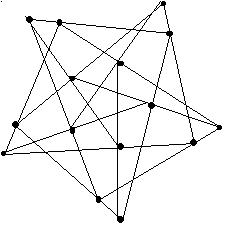
A k-configuration is a finite collection of n points and n lines, such that each of the n points is on precisely k lines and each line contains precisely k points. Some relevant results were known long ago, but the recent years have seen a large number of new results and novel problems. The development of the ideas will be sketched and some of the outstanding open questions described. A 3-configuration with n = 15 is shown below.
Venn diagrams are familiar to most of us. For example, we might draw a circle representing people who live in Nanaimo, and another overlapping circle representing University students, and where the intersection would consist almost entirely of VIU students. This diagram has two categories, residents of Nanaimo and University students.
But did you know that Venn diagrams exist for more than three categories? That they can be drawn symmetrically for an arbitrarily large numbers of categories? That they can be drawn nicely on a tennis ball? That there are many interesting unresolved problems about them? Problems that are easy to state and understand, but fiendishly difficult to solve?
In this talk we will review the interesting history of Venn diagrams, their basic properties, and some of their many practical uses. The talk will be lavishly illustrated with various Venn diagrams: some of historical note, some of practical utility, many of mathematical interest and many newly discovered.
In the upcoming volume of "The Art of Computer Programming", Don Knuth devotes 400 pages to the topic of combinatorial generation. Mathematically, the research area asks which combinatorial objects can be ordered by which basic operations. For example, the binary reflected Gray code shows that the binary strings of length n can be ordered by single bit changes [1946]. Binary strings of length n can also be ordered by removing the leftmost bit and inserting a new rightmost bit by de Bruijn cycles [1945]. As a third example, the permutations of any set are ordered by swapping adjacent elements in the Johnson-Trotter-Steinhaus order [1963]. Algorithmically, the research area asks how efficiently these orders can be generated.
This talk presents new results for a number of well-studied combinatorial objects. Algorithmic highlights include the first O(1)-time O(1)-space algorithm for generating the permutations of any multi-set, and the fastest algorithm for creating balanced parentheses strings (as determined by third-party tests). Mathematical highlights include shift Gray codes for ordered trees, the first Gray code for necklaces, and the first generalization of de Bruijn cycles to multiset permutations. The results are all based on a new variation on lexicographic order known as cool-lex order.
We will present some new results on partitioning both random and
non-random geometric covers. For the random results, let P be a Poisson
process of intensity one in the infinite plane R2, and surround each
point x of P by the open disc of radius r centered at x. Now let Sn
be a
fixed disc of area n >> r2, and let Cr(n)
be the set of discs which
intersect Sn. Write Erk for the event
that Cr(n) is a k-cover of Sn,
and Frk the event that Cr(n)
may be partitioned into k disjoint
single covers of Sn. We will sketch a proof
of the inequality
Prob(Ekr / Fkr)
<
Computer memories, at all levels of the hierarchy, have grown dramatically
over the past few years; however, increased problem size continues to
outstrip this growth. Most of the problem relates to structural information
such as search trees and permutations and relations used for indexing.
Nowhere is this issue more acute than in text search problems. Our interest,
then is in representations of combinatorial objects that are not only terse,
but also permit the basic operations one would expect on the underlying data
type to be performed quickly without decoding large portions of the data.
This type of representation is called a succinct data structure.
Several examples of succinct data structures will be discussed, including the
archetypal case of the binary tree. In this case we can reduce the storage
requirements from 3 or more words per node to about 2 bits per node, and still
perform the basic operations in constant time. We will also look at the limiting
tradeoffs between space constraints and navigating the structures quickly.
Ian Munro
Dept. of Computer Science, University of Waterloo
Monday, March 2, 10:00am, ECS 660
CAG
Schedule of Talks: Spring 2009
/ maintained by
Wendy Myrvold /
wendym@cs.UVic.ca
/ revised Apr. 28, 2009