A Cayley graph encapsulates the structure of a mathematical group generated by a given generating set.

Let \(H\) be a group. A set \(S \subseteq H\) is a generating set for \(H\), denoted by \(H = \left\langle S\right\rangle\), if every element \(h \in H\) can be represented as the product of elements of \(S\).

For a given group \(H\) and generating set \(S\), the Cayley graph of \(H\) generated by \(S\), denoted $\text{Cay}(H,S)$, is a graph \(G\) with \begin{aligned} V(G) &= H \\ E(G) &= \{\{h,hs\}: h \in H, s \in S\}. \end{aligned} Every vertex of \(G\) is an element of the group \(H\), and, for every generator \(s \in S\), edges are added between each element \(h\in H\) and the product \(hs\). Note that this definition results in an undirected graph; in other applications, Cayley graphs are often defined to be directed graphs.

The symmetric group on \(n\) elements, denoted \(S_n\), is the group of all permutations of \(1,2,\ldots, n\) under the operation of permutation composition. Permutations on this page are represented with disjoint cycle notation. For any \(n \geq 3\), the set $$\{(12), (23\ldots n)\}$$ is a generating set for \(S_n\). More generally, for \(2 \leq k \leq n-1\), the set $$B_{n,k} = \{(12), (23), \ldots, ((k-1),k), (k,(k+1), \ldots, n)\}$$ generates \(S_n\). The specific subset of Cayley graphs studied here will be the graphs $G_{n,k} = \text{Cay}(S_n,B_{n,k})$.

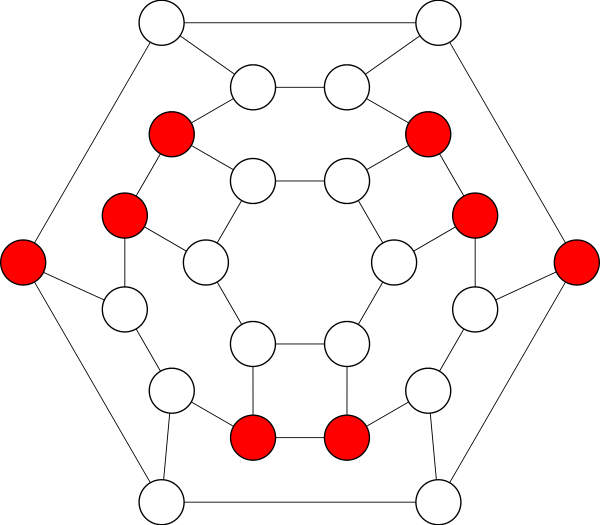
The diagram below shows the graph \(G_{4,3}\), with a minimum dominating set (of size 8) highlighted in red. The graph is isomorphic to a truncated octahedron.

Facts about $G_{n,k}$

• For all \(n \geq 3\), every graph \(G_{n,k}\) has \(n!\) vertices.
• For \(k \in \{2,3,\ldots, n-2\}\), \(G_{n,k}\) is \((k+1)\)-regular. When \(k = n-1\), \(G_{n,k}\) is \(k\)-regular.
• \(G_{3,2}\) is isomorphic to the 6-cycle \(C_6\), and \(\gamma(G_{3,2}) = 2\).
• When \(n \geq 3\) and \(k \geq 3\), the graph \(G_{n,k}\) contains \(n\) vertex-disjoint subgraphs isomorphic to \(G_{n-1,k-1}\) which partition the vertices of \(G_{n,k}\) (that is, every vertex of \(G_{n,k}\) lies in exactly one of the subgraphs). These subgraphs correspond to the cosets of \(S_{n-1}\) in \(S_n\).
• The previous point gives a simple recursive bound on the domination number of \(G_{n,k}\) when \(k \geq 3\): $$\gamma(G_{n,k}) \leq n\cdot\gamma(G_{n-1,k-1}).$$
• For \(n \geq 4\), the graph \(G_{n,2}\) contains \(n(n-2)!\) vertex disjoint copies of \(C_{n-1}\) (the cycle on \(n-1\) vertices) which partition the vertices of \(G_{n,2}\). Since \(\gamma(C_i) \leq \lceil \frac{i}{3}\rceil\), this gives the bound $$\gamma(G_{n,2}) \leq n(n-2)! \cdot \left\lceil \frac{n-1}{3}\right\rceil.$$
• Combining the two bounds above gives the general bound $$\gamma(G_{n,k}) \leq \frac{n!}{n-k+1}\left\lceil \frac{n-k+1}{3}\right\rceil \leq \frac{n!(n-k+4)}{3(n-k+1)}$$