CSC 482/582: Fall 2016 Assignment #2
Due at the beginning of class, Wednesday Oct. 12

Instructions for all assignments:

  1. Draw boxes for your marks on the top of the first page of your submission. Place a 0 in the corresponding box for any questions you omit. For this assignment:
    Question1234567 8 9 10
    Marks 0 0 0 0 0 0 0 0 0 0
  2. Questions must be submitted in order.
  3. Written submissions can be handed in up to 4 days late with a 10% penalty for each day past the deadline. If you want to submit your written work on a day that we do not have class, please write the day and time submitted on your first page and slip it under my office door (ECS 552).

  1. Consider a 6-cycle whose vertices are labelled in cyclic order with 0, 1, 2, 3, 4, 5.
    (a) [5] Write down the 12 permutations in cycle structure notation that are automorphisms which arise from rotating the 6-cycle or from flipping by applying the permutation (0)(15)(24)(3) and then rotating the 6-cycle.
    (b) [5] The 6-cycle has 6 places where a reflection results in an automorphism. These correspond to the following axes of reflection:
    Write down the permutations (using cycle structure notation) which correspond to R1-R6 and confirm that they already occur on your list from (a).

  2. One proof that a planar graph on at least three vertices has at most 3n-6 edges is as follows:
    If a planar graph has a maximum number of edges then all of the faces are 3-faces.
    Each edge is in exactly 2 faces. So 3 * f= 2 * m for a triangulated embedding.
    For an arbitrary embedding 3f <= 2m since all the faces have at least 3 edges.
    But by Euler's theorem, f= m-n+2 for a planar graph.
    Therefore, 3f = 3*(m-n+2) = 3m -3n + 6 <= 2m.
    Rearranging this algebraically gives: m <= 3n - 6.
    (a) [7] Come up with a similar argument which gives a tight upper bound on the number of edges that a planar bipartite graph can have (one definition of a bipartite graph is that it is a graph with no odd cycles).
    (b) [3] What if anything can you conclude about K3,3 from this argument?

  3. Observe that an independent set of G cannot contain more than n/2 vertices of each n-cycle of the graph.

    (a) [5] Show all the maximum independent sets of the graph on the Question 3 Worksheet (click here to get it, print as many copies as you need).

    (b) [3] Two independent sets are equivalent if there is an automorphism of the graph mapping one to the other. How many equivalence classes of maximum independent sets does this graph have? Justify your answer.

    (c) [2] For each equivalence class, choose the lexicographic minimum independent set as the representative of the class. For each representative independent set, which automorphisms of the graph map the independent set to itself?

  4. (a) [4] Prove that a fullerene on 22-vertices would have 12 5-faces and one 6-face.
    (b) [6] Start with the one 6-face in the center of a picture and try to complete the picture to a 22-vertex fullerene by adding 12 pentagons. What happens and what does this tell you about the existence of fullerenes on 22 vertices?

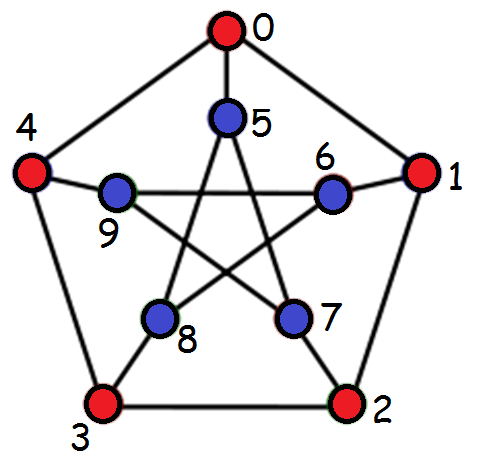
  5. [10] Consider the unique 24-vertex fullerene which likely arose as you were doing the previous question. Determine the order of the automorphism group and describe all the symmetries of this fullerene in terms of how they affect the cycles of the graph. What I am looking for is similar to when we described the symmetries of the dodecahedron by noting that any 5-cycle can map to a given one in 10 different ways (5 rotations, or flip and consider the 5 rotations) and since there are 12 5-cycles, the order of the group is 12*10= 120. You don't need to write down all the permutations in the automorphism group.

  6. The Petersen graph looks like this:

    (a) [3] Draw a picture of the graph that corresponds to this uniform voltage graph.

    (b) [2] Is the graph from part (a) isomorphic to the Petersen graph? Justify your answer.
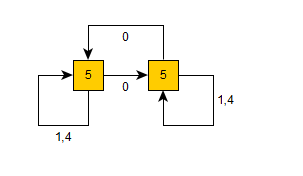
    (c) [3] Draw a picture of the graph that corresponds to this non-uniform voltage graph.

    (d) [2] Is the graph from part (c) isomorphic to the Petersen graph? Justify your answer.

  7. [5] Draw the tree which arises from the trivial lower bound on the number of vertices that a (3,7)-cage must have. How many vertices are at distances 0, 1, 2, and 3 from the root?
    Important note for error checking on the next question: the McGee graph has 24 vertices and the extra ones are at distance 4 from the root.

    The McGee graph:

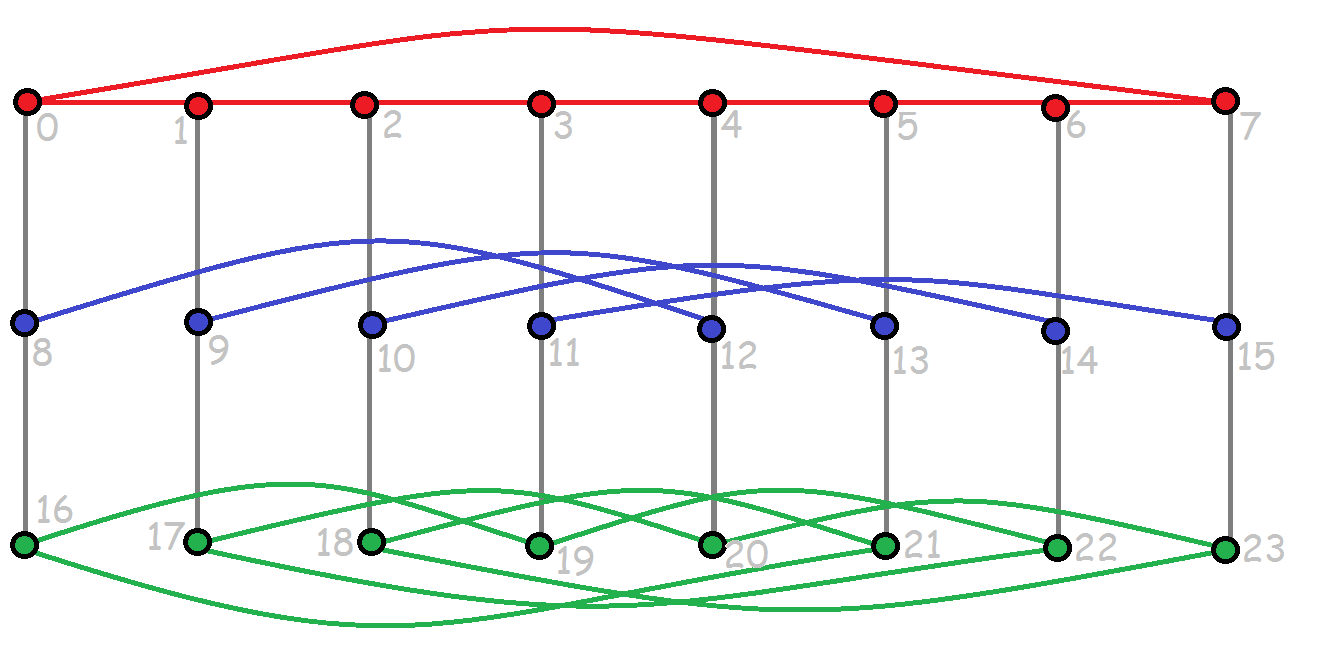
  8. The purpose of this question is to explore the structure of the McGee graph. The results for this question will help you to complete the next question.

    Put your answers on the attached Question 4 worksheet.

    (a) [3] Do a BFS on the McGee graph starting at the leftmost red vertex (vertex 0). What I want you to indicate on the picture is just the distance of each vertex from the root of the BFS tree. The starting vertex is at distance 0 from itself. For error detection: ensure you have the correct counts as per the previous question.

    (b) [4] Do a BFS on the McGee graph starting at the leftmost blue vertex (vertex 8). What I want you to indicate on the picture is just the distance of each vertex from the root of the BFS tree.

    (c) [3] Do a BFS on the McGee graph starting at the leftmost green vertex (vertex 16). What I want you to indicate on the picture is just the distance of each vertex from the root of the BFS tree.

  9. With the vertex labelling indicated in the picture above, it is clear that
    (0 1 2 3 4 5 6 7)(8 9 10 11 12 13 14 15)(16 17 18 19 20 21 22 23)
    is an automorphism of the graph. The aim of this question is to determine if some other symmetries are present.

    (a) [4] Does the McGee graph have an automorphism which maps some red vertex to a blue vertex? If your answer is yes, show the automorphism on the attached Question 5(a) worksheet. If you say no, justify your answer. Hint: consider the vertices at distance 4 from the root of the BFS tree from your answers from the previous question.

    (b) [4] Does the McGee graph have an automorphism which maps some red vertex to a green vertex? If your answer is yes, show the automorphism on the attached Question 5(b) worksheet. If you say no, justify your answer.

    (c) [4] Does the McGee graph have a symmetry which reverses the top 8-cycle? That is, the symmetry starts out like this:
    (0) (1 7) (2 6) (3 5) (4) ...
    If your answer is yes, show the automorphism on the attached Question 5(c) worksheet. If you say no, justify your answer.

    (d) [3] What is the automorphism group order of the McGee graph? Hint: the only types of symmetries it has are the types you have explored so far. Explain your answer in terms of what the symmetries do to the vertices of the graph.

  10. Given a fixed root vertex v, the edges of the McGee graph can be divided into classes:
    1. The edges which are in the BFS tree of v that goes down to the vertices at distance at most 3 from v.
    2. Chords connecting pairs of vertices at distance 3 from v.
    3. Edges between one vertex at distance 3 from v and another one at distance 4.
    4. Edges between two vertices at distance 4.
    The number of edges in class 1 is the same for every vertex since the graph is a (3,7)-cage. The numbers in classes 3 and 4 are easy to see. From there you can get the number of chords. The 7-cycles which include vertex v are in one to one correspondence with these chords since every 7-cycle has a unique edge such that both of its endpoints are at distance 3 from v.

    (a) [1] Apply the hints above to count the number of 7-cycles containing one specific red vertex.

    (b) [1] Apply the hints above to count the number of 7-cycles containing one specific blue vertex.

    (c) [1] Apply the hints above to count the number of 7-cycles containing one specific green vertex.

    (d) [7] Use the information from parts (a), (b) and (c) to determine the number of 7-cycles in the McGee graph.

CSC 482B/582B Assignments / maintained by Wendy Myrvold / wendym@cs.UVic.ca / revised Sept. 29, 2016