Enumerating tatami mat arrangements of square grids with $v$ vertical dimers
Alejandro Erickson,
Department of Computer Science,
University of Victoria, Canada.
Frank Ruskey,
Department of Computer Science,
University of Victoria, Canada.
Abstract:
Let $\mathbf{T}_{n}$ be the set of monomer-dimer tatami tilings of the
$n\times n$ grid with the maximum number, $n$, of monomers, and which have a
monomer in each of the top left and top right corners. We consider
those tilings of $\mathbf{T}_n$ with exactly $v$ vertical dimers and prove
that their numbers are the coefficients of the polynomial
\begin{align}
\label{eq:tnzIntro}
V\hspace{-5pt}H_n(z):=2\sum_{i=1}^{\lfloor (n-1)/2 \rfloor}
S_{n-i-2}(z)S_{i-1}(z)z^{n-i-1} +
\left(S_{\lfloor (n-2)/2 \rfloor}(z)\right)^2,
\end{align}
where $S_n(z)$ is the generating function of the number of subets of
$\{1,2,\ldots, n\}$ whose members sum to $k$. Furthermore,
$V\hspace{-5pt}H_h(z)$ has the factorization
\begin{align*}
P_n(z)\prod_{j\ge 1} S_{\lfloor (n-2)/2^j \rfloor}(z),
\end{align*}
where $P_n(z)$ is a somewhat mysterious polynomial with several
observable patterns. We show for all $n\ge 2$, that $P_n(1) =
n2^{\nu(n-2)-1}$, where $\nu(n)$ is the number of $1$s in the binary
representation of $n$ and that $\deg(P_n(z)) = \sum_{k=1}^{n-2} \text{Od}(k)$,
where $\text{Od}(k)$ is the largest odd divisor of $k$. In
addition $P_n(z)$ is irreducible and
\begin{align*}
\sum_{n\ge 2} P_n(-1)z^{n-2} = \frac{(1+z)(1-2z)}{(1-2z^2)\sqrt{1-4z^2}},
\end{align*}
at least for $2\le n < 200$.
The combinatorial decomposition underlying the polynomial
$ V\hspace{-5pt}H_n(z)$ leads to an algorithm for exhaustively generating these
tilings in constant amortized time per tiling.
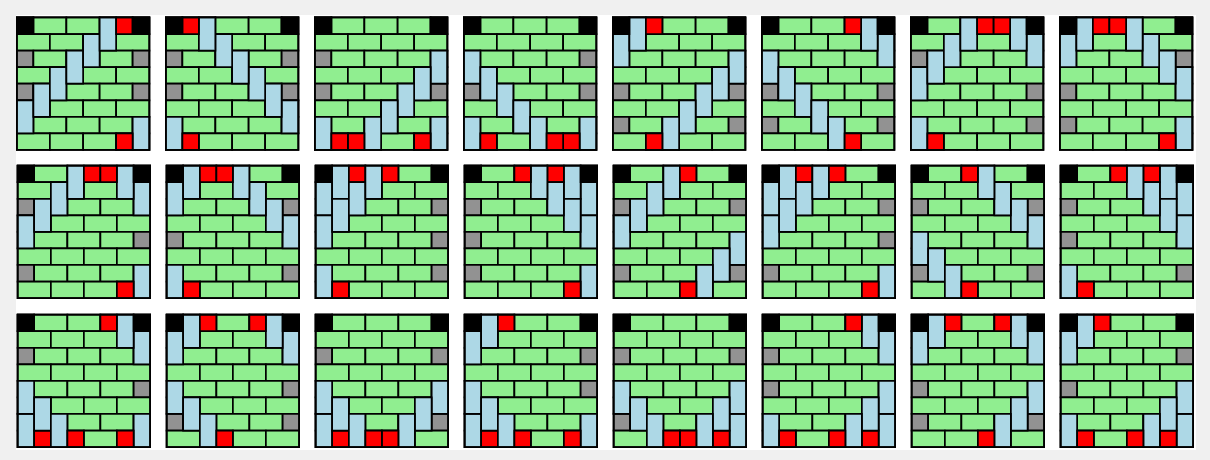
Below we show all tilings in $\mathbf{T}_8$ with $7$ vertical dimers.
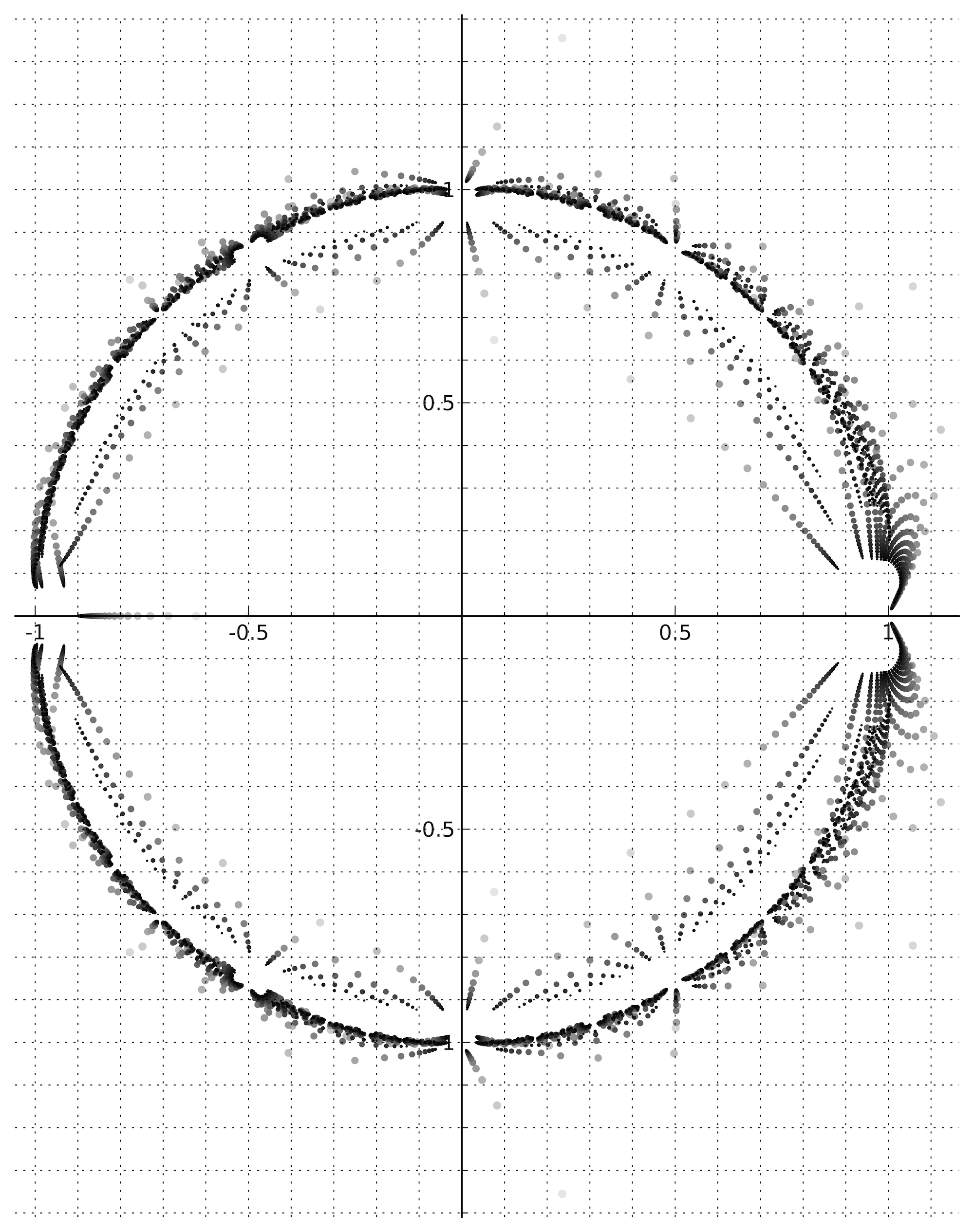
The plots below show the roots of the polynomial $P_n(z)$ for $n$ even on the left and
for $n$ odd on the right. In both cases $3 \le n \le 49$.
Darker and smaller points are used for larger values of $n$.
Clicking on the image will bring up a (much) larger image of the respective plot.
-
Download: pdf file (not yet).
-
Submitted ??? ??, 2012.
-
Please send me a note if
you download one of these files.
It's always nice to know who's reading your papers.
-
Selected citations:
Back to list of publications.