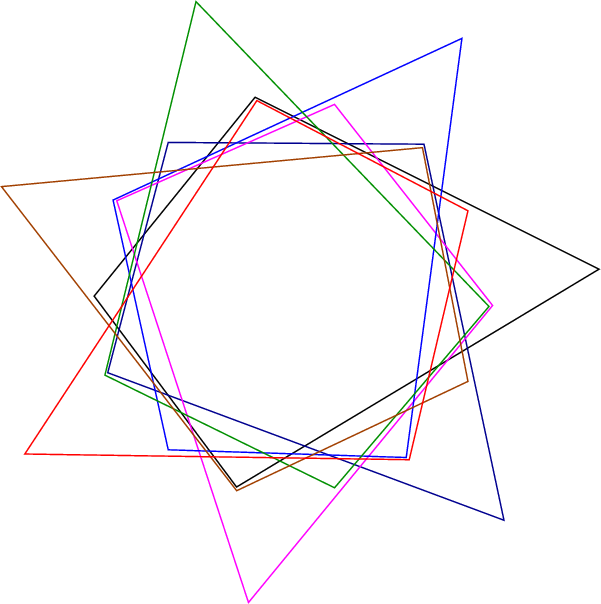
Which <I>n</I>-Venn diagrams can be drawn with convex <I>k</I>-gons?

Which n-Venn diagrams can be drawn with convex k-gons?

Jeremey Carroll, HP Labs, Bristol, England.
Frank Ruskey, Department of Computer Science, University of Victoria, Canada.
Mark Weston, Department of Computer Science, University of Victoria, Canada.

Abstract:

We establish a new lower bound for the number of sides required for the component curves of simple Venn diagrams made from polygons. Specifically, for any n-Venn diagram of convex k-gons, we prove that k > ( 2ⁿ - 2 - n ) / ( n (n-2)). In the process we prove that Venn diagrams of seven curves, simple or not, cannot be formed from triangles. We then give an example achieving the new lower bound of a (simple, symmetric) Venn diagram of seven quadrilaterals. Previously Grünbaum had constructed a 7-Venn diagram of non-convex 5-gons ["Venn Diagrams II", Geombinatorics 2:25-31, 1992].

The pdf file.
The postscript file.
Please send me a note if you download one of these files. It's always nice to know who's reading your papers.
Presented at the 2nd Workshop on Euler Diagrams, Paris, September 29-30, 2005.
Appear in Discrete and Computational Geometry, 37 (2007) 619-628. (submitted 17/03/2006, accepted 23/09/2006).
Below we show a 7-Venn diagram made from 4-gons. Such a diagram was not known to exist previously.

Back to list of publications.