Minimum Area Venn Diagrams whose Curves are Polyominoes

Stirling Chow, Department of Computer Science, University of Victoria, Canada.
Frank Ruskey, Department of Computer Science, University of Victoria, Canada.

Abstract:

Venn diagrams are collections of simple closed curves in the plane with the property that intersection of the interiors of any subcollection of the curves must be a non-empty connected region. Here we consider the curves to be the boundaries of polyominoes. If there are n polyominoes, then in a minimum area Venn diagram the area of each polyomino is 2^n-1. We give examples of minimum area Venn diagrams for n = 2,3,4,5,6,7 and an approximation algorithm that gives Venn diagrams of asymptotically minimum area.

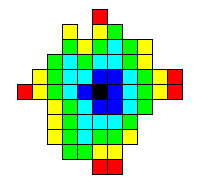
Example:

The example below consists of 6 polyominoes and how they should be placed relative to each other to form a minimum area Venn diagram.

For the example above, we show below a coloring of each region of the Venn diagram according to how many polyominoes cover that square: red = 1, yellow = 2, green = 3, cyan = 4, blue = 5, and black = 6.

The pdf file.
The postscript file.
Please send me a note if you download one of these files. It's always nice to know who's reading your papers.
Appears in Mathematics Magazine, Volume 80, No. 2, April 2007, pp. 91-103.
Submitted March 2, 2005.
Mark Thompson's page on Venn Polyominos is what got us started on this research.
For more on Venn diagrams check out the Survey of Venn Diagrams, Dynamic Survey #5 at the Electronic Journal of Combinatorics.
A relevant reference that we should have included is David W. Henderson, Venn diagrams for more than four classes, American Mathematical Monthly, American Mathematical Monthly, 70 (1963) 424–426. That paper contains the necessary condition that n is prime in any symmetric n-Venn diagram.

Selected papers that refer to this one:

Ed Pegg's August 2006 Mathpuzzle column.
Wolfram Demonstrations Project: The Chow-Ruskey Order 5 Venn Diagram.

Several of the open problems posed in this paper have been solved. Except where noted all of the diagrams linked below are due to Bette Bultena.

A 3x5 diagram (no empty set): link. Note that all the polyominoes are convex.
A 7x9 diagram (no empty set): link.
An 8x8 diagram: link.
Another 8x8 diagram (by Abdolkhalegh Ahmadi): link. Note that the rightmost 4 columns form the 4x8 diagram from the paper.
An 8x16 diagram: link.

News Flash!

Several of the open problems in the paper have been solved by a nice construction of Matthew Klimesh, and by some constructions of Bette Bultena inspired by those of Klimesh. In particular, minimum area Venn diagrams exist for all n, and they can be put in boxes of various aspect ratios. These constructions will be written up in a paper in due course, but for now, here are some teasers!

Back to list of publications.