Simple Spherical Venn diagrams with Isometry Groups of Order Eight
Khalegh Mamakani,
Department of Computer Science,
University of Victoria, Canada.
Frank Ruskey,
Department of Computer Science,
University of Victoria, Canada.
Abstract:
For each n > 4 we show how to construct simple Venn diagrams of n curves embedded on the sphere with the following sets of
isometries: (a) a 4-fold rotational symmetry about the polar axis, together with an additional involutional symmetry about an
axis through the equator, and (b) an involutional symmetry about the polar axis together with two reflectional
symmetries about orthogonal planes that intersect at the polar axis.
In both cases (a) and (b) the order of the group of isometries is 8.
Examples
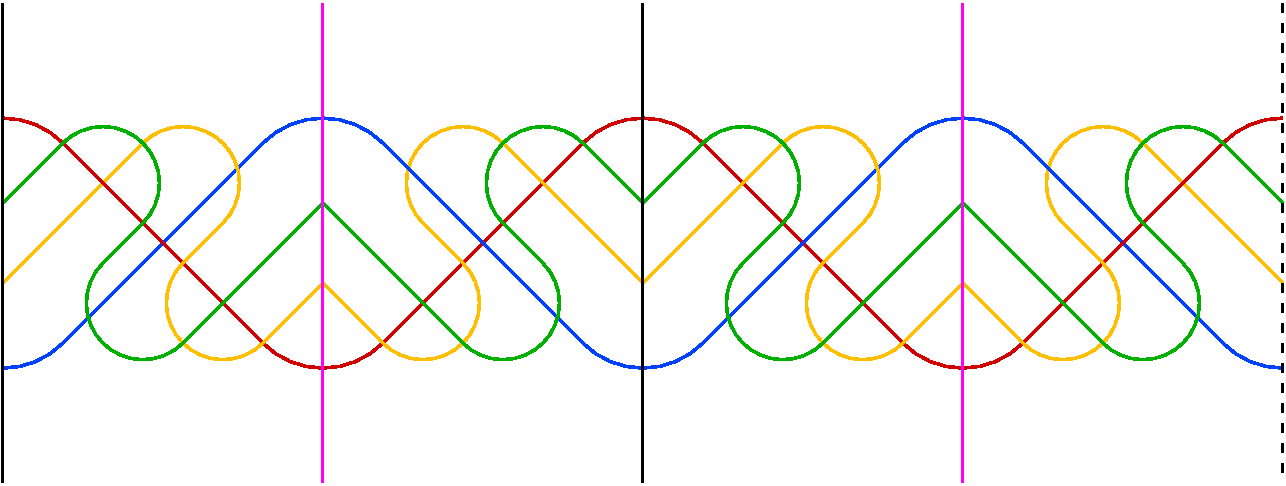
Below we show two examples of our construction for n = 6 curves.
These are cylindrical representations of the diagrams.
In the first diagram there is four-fold rotational symmetry about
the polar axis (note that two curves pass throught the north and
south poles in both diagrams). There is also and axis of symmetry
through the equator (e.g., antipodal points where the
red and blue curves intersect).
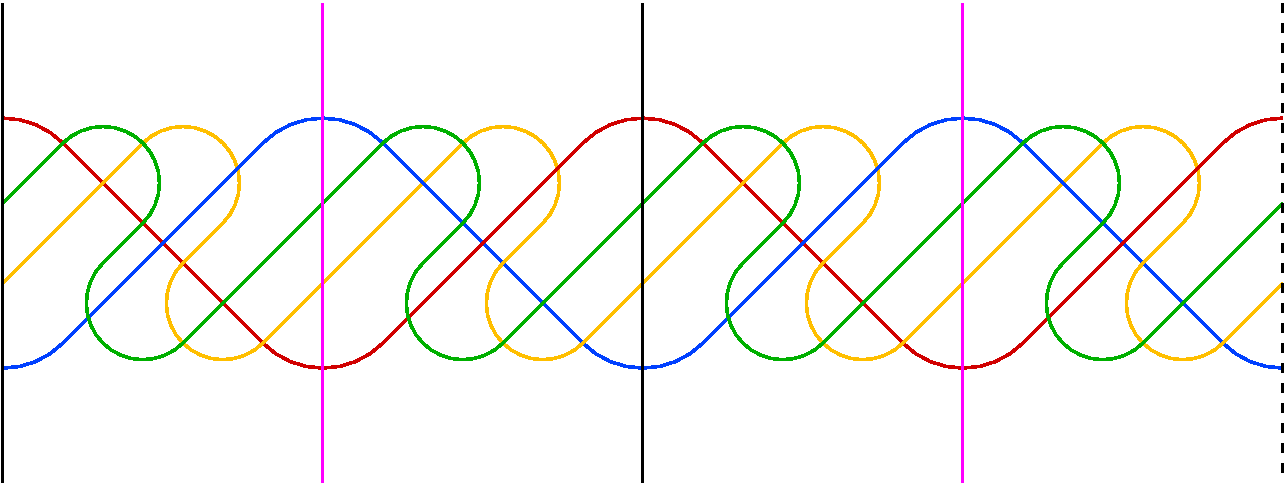
In the second diagram there are reflectional symmetries about
two orthogonal planes whose intersection is the polar axis.
As in the previous diagram, there is also and axis of symmetry
through the equator (e.g., antipodal points where the
red and blue curves intersect).