Planar Graphs

In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other(from wikipedia).

3-regular Planar Graph Generator

1. Description

We generate all the 3-regular planar graphs based on K4. Referred to the algorithm M. Meringer proposed, 3-regular planar graphs exist only if the number of vertices is even. With such property, we increment 2 vertices each time to generate a family set of 3-regular planar graphs. Here is the basic idea of the algorithm :

Random regular planar graphs are generated using a rotation system. A rotation system means that the graph is represented in an adjacency list that has the clockwise order for the neighbours of each vertex. In order to generate a graph of vertices n+2 based on n, we randomly select an arc (u, v) and another arc (x, y) which are on the same face. Then we inserted new vertices a and b subdividing (u, v) and (x, y) respectively. Connecting a and b creates a new graph of vertices n+2. We iterates this process and create a family of 3-regular planar graphs.

2. Source code and usage

The implementation is attached at di_gen.c. To use this generator, compile it with GCC with the following command:

$ gcc di_gen.c -o di_gen

To run the generator. Run the executable file di_gen.exe followed by two arguments: min_n and max_n

$ ./di_gen min_n max_n

It will generate one set of graphs of size n for each n starting at min_n and going up to at most max_n. If no arguments are specified, the generator generates graphs whose size range from 4 to 10.

3. Graph outputs

For each graph, the output format is as follows:

(line 1): number of vertices n_nodes
(line 2 to line (n_nodes -1)): each line starts with degree u, and followed by the list of neighbours of that particular vertex.

A example of the output graph is attached below:

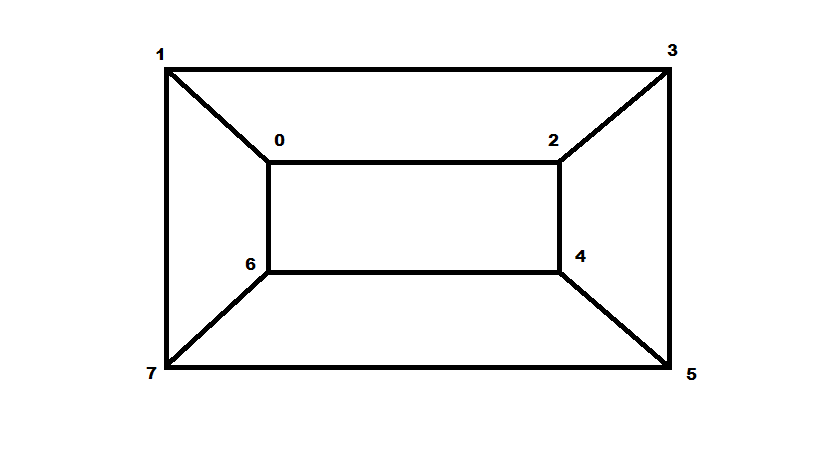
To generate such a graph, use the following command*

./di_gen 8 8

*Please note that the vertices order might not be the same as the example.
We generated a set of 9 graphs (vertices from 40 to 50, and 80, 90, and 96 separately)di_randGraphs.txt and we listed the dominating set tests of them as follows:

Graph NO.	Num of Vertices	Size of Min. Dom Set	Time
1	40	11	0.047s
2	42	11	0.062s
3	44	12	0.094s
4	46	12	0.062s
5	48	13	0.188s
6	50	13	0.234s
7	80	22	75.13s
8	90	24	25.35s
9	96	26	51.54s

4. Certificates

4. Certificate to the output is attached at di_randGraphs_cert.txt