Degree/Diameter graph

Content:

1. Definition
2. Application
3. Examples
4. References

Definition:

In graph theory, the diameter of a graph is defined as a the maximum distance of the shortest path between any pair of vertices; the degree of a vertex is defined as the number adjacent vertices; and the girth is the length of the shortest cycle contained in a graph.

The degree/diameter problem refers to find the largest possible graph, in terms of the number of vertices, with constraints in the  diameter (D) of the graph and the maximum degree (Δ)  of each vertex. The graph that meets this constraints are denoted as (Δ,D) graph.

Additionally, the order of a (Δ,D) graph with degree Δ > 2, and a diameter D is bounded by the Moore bound (an equivalent definition is a graph of diameter D and girth 2D+1).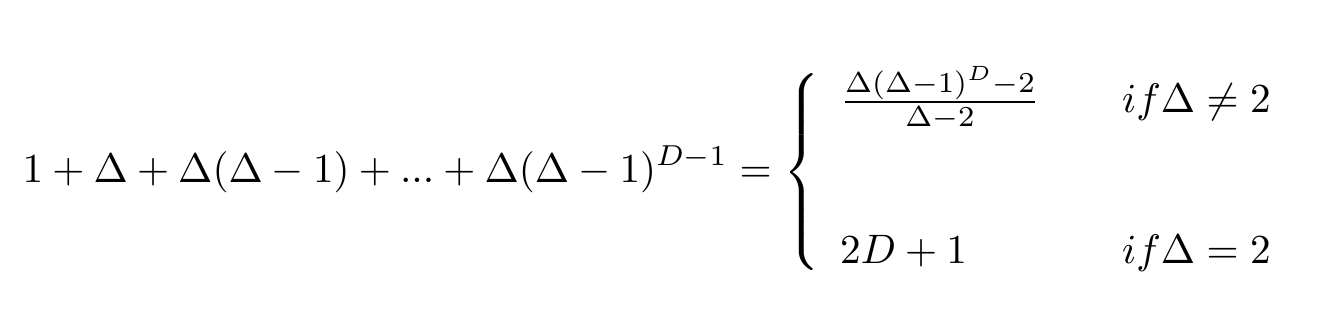

However, most of the degree diameter graph found until now are smaller than the Moore bound. The knowing graphs that meets the upper Moore bound are:

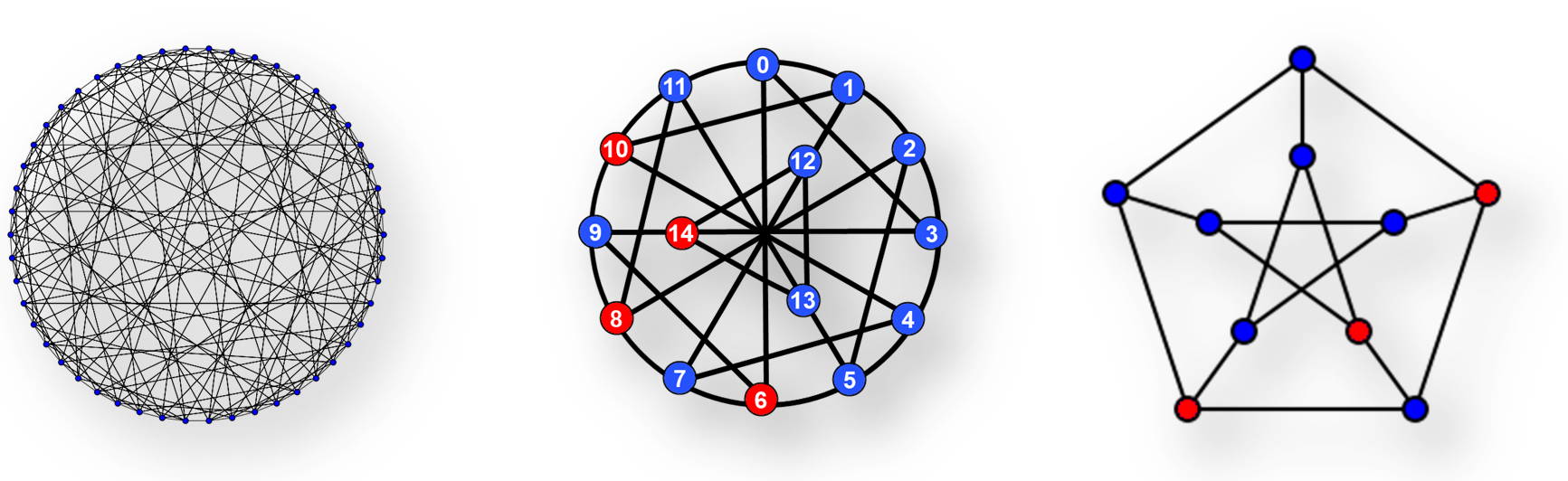Figure 1: Hoffman- Singleton (Left) [1], K3*C5 graph [2], and its dominating set (centre), and Petersen graph [2], and its dominating set in red (Right)

Given that this problem is computational hard researchers around the world keep a database with the graphs that meets the requirements. Some examples of  research that try to tackle this problem are [Ami2009, Jaj2009, Asa2010, Kon2005] .

(Δ,D) Application:

The degree/diameter graphs are used mostly in network related problems where the number of connections attached to each node is limited  (Δ), and the number of intermediate nodes should be small to meet timing tolerance [Din1994, Mil2005].

Other authors aim to solve two different problems at the same time, mixing the degree/diameter problem with another extra restriction. For example, taking into account the cost of the network, improve the parallel and distributed processing of a network, or construct a network to be faulttolerant [Dek2012, Rav2001]

Similarly, other authors applied the degree/diameter problem to different areas of knowledge. That is, Sohaee and Forst  [Sah2009]  tried to find the core of a network of interacting proteins by applying the bounded-diameter subgraphs.

Examples:

The files provided in this section belong to a different (Δ,D)-graphs. Each file was extracted from the website Applied Mathematics IV. What we did was change the format of the adjacency matrix files to fit  the requirements of our format, that is the following: 15 The graph has 15 vertices 4 1 3 6 11 Vertex 0 has 4 neigbours {1,3,6,11} 4 0 2 12 10 Vertex 1 has 4 neigbours {0,2,12,10} 4 1 3 5 8 Vertex 2 has 4 neigbours {1,3,5,8} 4 0 2 4 14 Vertex 3 has 4 neigbours {0,2,4,14} 4 3 5 7 10 Vertex 4 has 4 neigbours {3,5,7,10} 4 2 4 6 13 Vertex 5 has 4 neigbours {2,4,6,13} 4 0 5 7 9 Vertex 6 has 4 neigbours {0,5,7,9} 4 4 6 8 12 Vertex 7 has 4 neigbours {4,6,8,12} 4 2 7 9 11 Vertex 8 has 4 neigbours {2,7,9,11} 4 6 8 10 14 Vertex 9 has 4 neigbours {6,8,10,14} 4 1 4 9 11 Vertex 10 has 4 neigbours {1,4,9,11} 4 0 8 10 13 Vertex 11 has 4 neigbours {0,8,10,13} 4 1 7 13 14 Vertex 12 has 4 neigbours {1,7,13,14} 4 5 11 12 14 Vertex 13 has 4 neigbours {5,11,12,14} 4 3 9 12 13 Vertex 14 has 4 neigbours {3,9,12,13}

References: