My Interesting Graph: Moore Graph
Among all the regular graphs, Moore Graph is well-known for its maximum possible number of nodes with low diameter.
In graph theory, a Moore graph of type (d,k) is a regular graph on n vertices with degree d and diameter k for which n equals
Hoffman and Singleton originally defined the term "Moore graph" as a graph at related regular graph of given vertex degree d and diameter k.
The interesting part about Moore graph is that they proved for k = 2, Moore graph exist only when it is type of (2,2), (3,2), (7,2) and possibly (57,2),
and (57,2) still remains an unsolved problem up to today. For k = 3, the only Moore graph is (2,3).
Why
Beauty is rare! The nature of symmetry and uniqueness in Moore graph is an fascinating factor that makes it a interesting topic to me.
What
The file I put up here is a small samples of generalized Moore graph (presented in adjacency list), they are the following graphs:
1. pertersen graph
2. K7 complete graph
3. c8 circle graph
4. Heawood graph
Dominating Sets for them
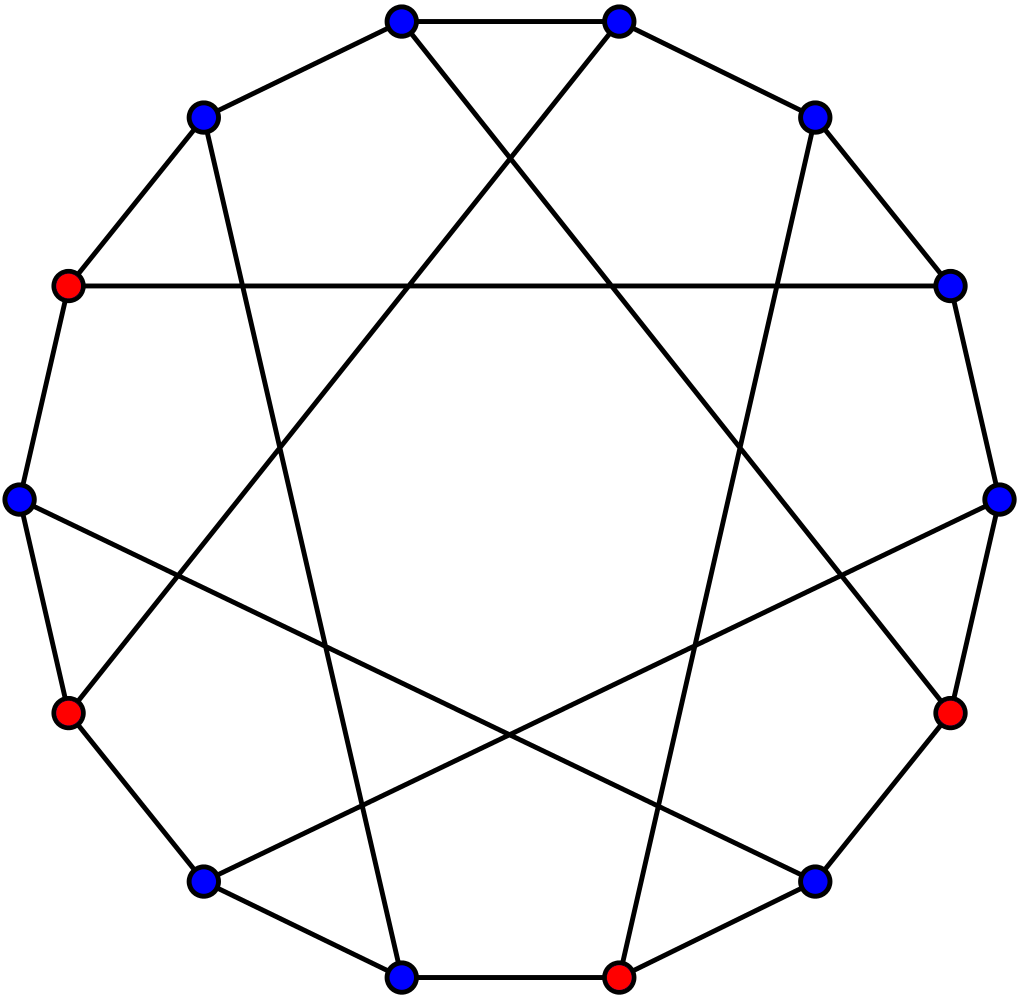
However, after I realize the nature of Moore graphs, I think the searching for dominating sets in those graphs are pretty straightforward since
every node has same degree.
