|
1. Definition
In graph theory a cage is a regular graph (i.e., each vertex has the same number of adjacent vertexes) that has as few vertices as possible for its girth (i.e. the length of a shortest cycle contained in the graph).
As a definition, is a (v,g)-cage graph one which each vertex has exactly v neighbours and a girth g [1,2].
There are multiple cage graphs. 3-regular cages are those in the form (3,g)-cage (i.e., v is equals to 3) also known as small cages [3]. Table 1 summarizes well known 3-regular cages [1].
|
(v,g) | Named cages Vertices | (Order) |
| (3,3) | Complete graph K 4 | 4 |
| (3,4) | Complete bipartite graph K (3,3) | 6 |
| (3,5) | Petersen graph | 10 |
| (3,6) | Heawood graph | 14 |
| (3,7) | McGee graph | 24 |
| (3,8) | Levi graph | 30 |
| (3,9) | Biggs and Hoare (1980), Brinkmann et al. (1995) | 58 |
| (3,10) | Balaban 10-cage, Harries graph, Harries-Wong graph | 70 |
| (3,11) | Balaban 11-cage; Balaban (1973), Myrvold and McKay | 112 |
| (3,12) | Tutte 12-cage; Polster et al. (1998, p. 179) | 126 |
Table 1. 3-regular known cage graphs [3]
|
One of the most popular, the Petersen graph which is a Moore graph depicted in Figure 1.
Figure 1. The Petersen graph as a Moore graph.
In fact the properties of Moore graphs generalize to cages. . That is, the number of vertices of a cage is:
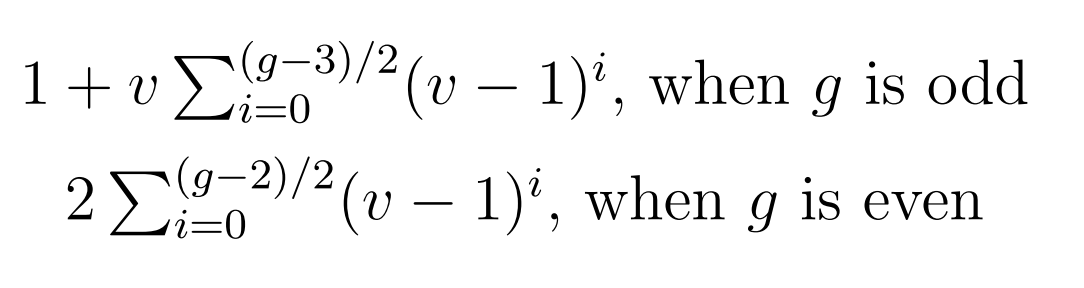Another example, depicted in Figure 2 depicts the Heawood graph highlighting its minimum dominating set D={5,7,10,12}.
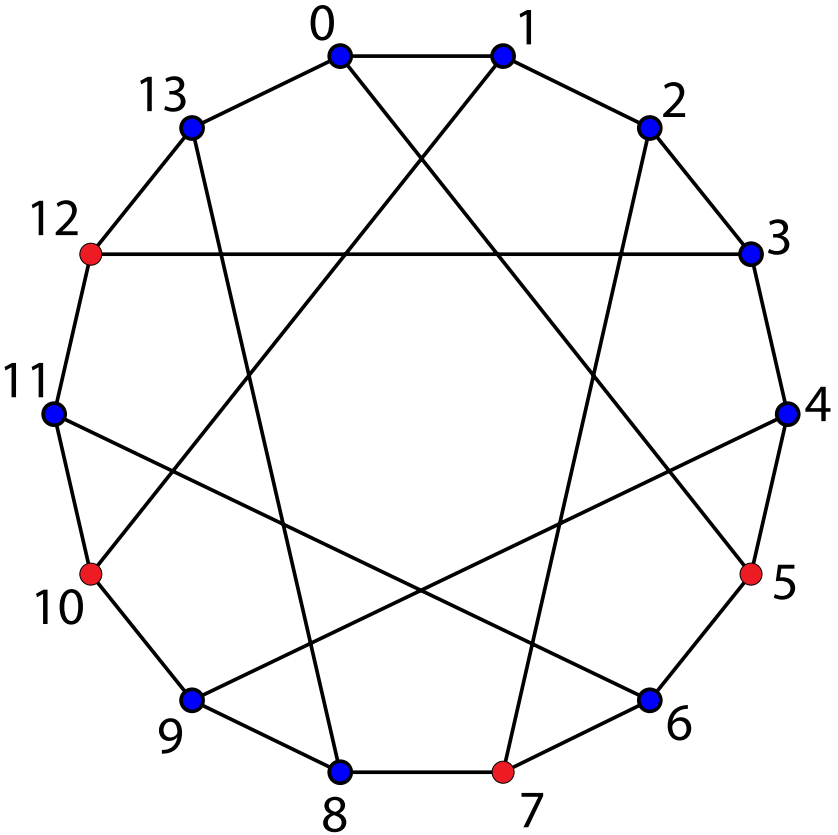
Figure 2. The Heawood graph with its dominating set (Red vertexes)
2. Interesting graphs
Cages are interesting grapsh for its networking applications, especially Atici et al. uses the integrity of a graph to ensure reliability of the network communication capabilities [4]. The integrity of a graph G(V,E) is defined as:
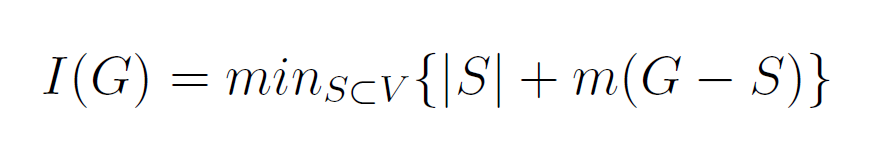
In their approach, the authors present a network that is modelled as a graph in which by deleting few vertices and taking it into its smallest possible size, the integrity can be measured.
Similarly, (3,g)-cages have a particular application in the mathematical chemistry to model isoprenoid structures, benzenoid polycyclic hydrocarbons, and topological indices. In the approach Table 2 presented by Balaban, summarizes some trivalent polyhedra and cages symmetry examples used to represent the chemistry automorphism groups using graphs [5].
| Polyhedron (V,O) | (3,g)-Cage |
| Tetrahedron (4,12) | (3,3)-cage K4 |
| Cube (8,24) | (3,4)-cage K(3;3) |
| Pentagonal prism (10,20) | (3,5)-cage Petersen |
| Dodecahedron (20,60) | (3,6)-cage Heawood |
| Truncated tetrahedron (12,36) | (3,7)-cage McGee |
| Truncated cuboctahedron (48,144) | (3,12)-cage Tutte |
Table 2. Some polyhedra and -cages symmetry groups [2]. (Legend. V:Vertices, O:Order) [5]
3. Cages files
(3,3)-cage example
|
The following files correspond to different (v,g)-cages. Each file is in the following format:
The First line corresponds to the number of vertices (n) in the graph
The Following n lines are the vertexes (v) and its neighbours if the following format:
The first digit corresponds to the degree (d) of v, and the next d numbers are the neigbours of v.
For example the (3,3)-cage file presents the following structure:
| 4 | | | -----> The graph has 4 vertexes |
| 3 | 1 | 2 | 3 ---> Vertex 0 has 3 neigbours {1,2,3} |
| 3 | 0 | 2 | 3 ---> Vertex 1 has 3 neigbours {0,2,3} |
| 3 | 0 | 1 | 3 ---> Vertex 2 has 3 neigbours {0,1,3} |
| 3 | 0 | 2 | 1 ---> Vertex 3 has 3 neigbours {0,2,1} |
|
Files
| Download | --- (3,3)-cage |
| Download | --- (3,4)-cage |
| Download | --- (3,5)-cage |
| Download | --- (3,6)-cage |
| Download | --- (3,7)-cage |
| Download | --- (3,8)-cage |
| Download | --- (3,9)-cages |
| Download | --- (3,10)-cage of 80 vertices |
| Download | --- (3,10)-cage Balaban |
| Download | --- (3,10)-cage Harries |
| Download | --- (3,10)-cage Wong |
| Download | --- (3,11)-cage |
| Download | --- (3,12)-cage |
References
-
Eric Weisstein at Wolfram Research. Cage graph. http://mathworld.wolfram.com/CageGraph.html.
-
Tomaz Pisanski and Brigitte Servatius. Graphs. In Configurations from a Graphical Viewpoint, Birkhauser Advanced Texts Basler Lehrbucher, pages 15–53. Birkhauser Boston, 2013. (Book)
-
Geoffrey Exoo and Robert Jajcay. Dynamic cage survey. The electronic journal of combinatorics, 16, July 2008. (Survey)
-
R. Crawford M. Atici and C. Ernst. The integrity of small cage graphs. The Australasian Journal of Combinatorics, 43:39, 2009. (Article)
-
Alexandru T. Balaban. Mathematical chemistry: (3,g)-cages with girth g, topological indices, and other graph-theoretical problems. Fundamenta Informaticae - Contagious Creativity, 64(1-4):1{16, 2004. (Article)
|