CSC 482/582: Fall 2012 Assignment #1
Due at the beginning of class, Thursday Nov. 15

Questions must be submitted in order.

1. On the attached worksheet for Question 1: Apply clockwise BFS to this graph with root vertex 0, first child 1, and direction clockwise to create a BFS tree.

   (a) [2] Label the remaining vertices with 2, 3, ... according to their Breadth-First indices.

   (b) [2] Colour the BFS tree arcs with a GREEN pen and direct these arcs so that the arc for each vertex u is directed from u to the parent of u in the BFS tree.

   (c) [4] Complete this to a Pfaffian orientation by colouring the remaining directed edges with a RED pen.

   (d) [2] Number the red edges 1, 2, 3, ... in the same order as you used when making your decisions about how to orient the edges.

2. Consider the following Pfaffian orientation of a graph G:

   

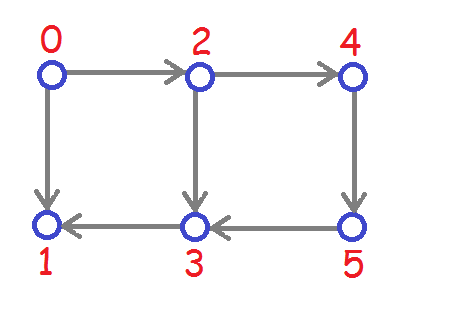
   (a) [3] List all the perfect matchings of G.

   (b) [3] Write down the skew-symmetric adjacency matrix A which corresponds to this Pfaffian orientation. Note: skew symmetric means that if a_i,j = c, then a_j,i = -c.

   (c) [8] Compute the determinant of your matrix from (c) by applying Gaussian elimination to the matrix until it is upper triangular keeping track of what each operation is doing to the determinant as you go along. Make sure you indicate what you are doing at every step, and how it affects the determinant.

   (d) [6] Which non-zero terms of the determinant correspond to having a pair of matchings where the first one is the matching which contains the edge (2,3)? Show the corresponding sub-matrices of A and for each one, draw the pair of perfect matchings with the edges of the first matching colored red and the edges of the second matching colored blue.

3. [10] Draw the tree which arises from the trivial lower bound on the number of vertices that a (3,7)-cage must have. How many vertices are at distances 0, 1, 2, and 3 from the root?
   Important note for error checking on the next question: the McGee graph has 24 vertices and the extra ones are at distance 4 from the root.

   ---

   The McGee graph:

   

4. The purpose of this question is to explore the structure of the McGee graph. The results for this question will help you to complete the next question.

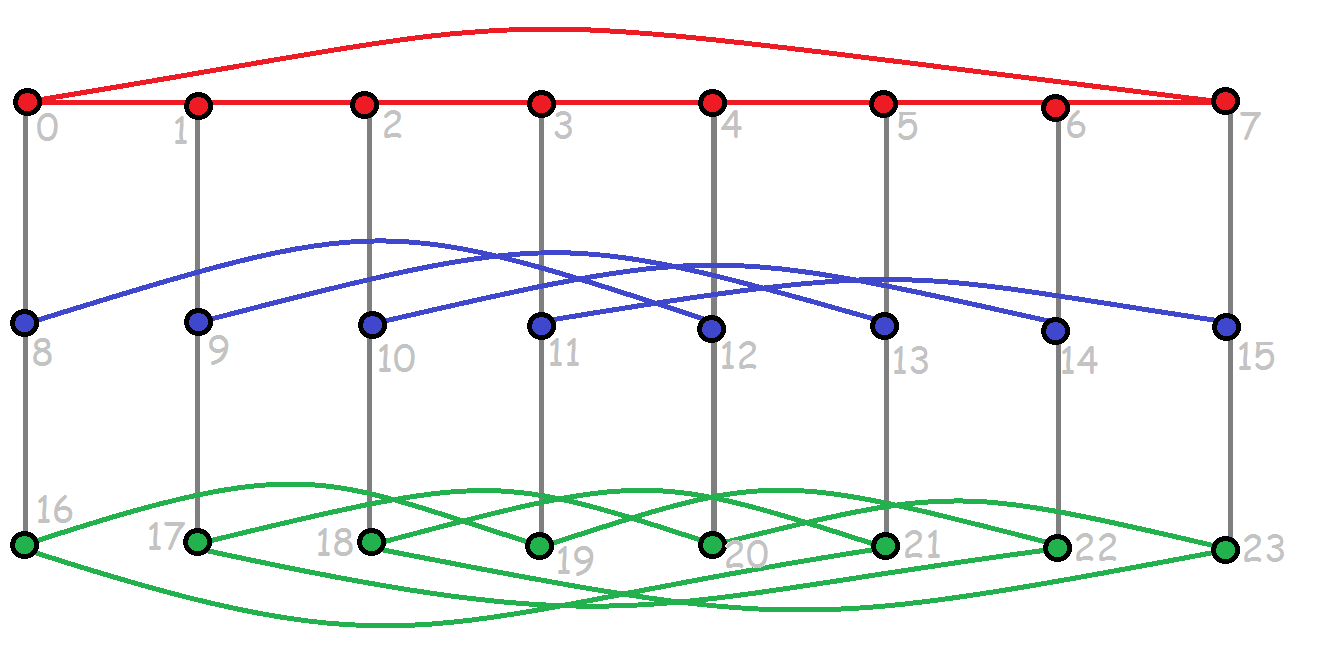
   Put your answers on the attached Question 4 worksheet.

   (a) [3] Do a BFS on the McGee graph starting at the leftmost red vertex (vertex 0). What I want you to indicate on the picture is just the distance of each vertex from the root of the BFS tree. The starting vertex is at distance 0 from itself. For error detection: ensure you have the correct counts as per the previous question.

   (b) [4] Do a BFS on the McGee graph starting at the leftmost blue vertex (vertex 8). What I want you to indicate on the picture is just the distance of each vertex from the root of the BFS tree.

   (c) [3] Do a BFS on the McGee graph starting at the leftmost green vertex (vertex 16). What I want you to indicate on the picture is just the distance of each vertex from the root of the BFS tree.

5. With the vertex labelling indicated in the picture above, it is clear that
   (0 1 2 3 4 5 6 7)(8 9 10 11 12 13 14 15)(16 17 18 19 20 21 22 23)
   is an automorphism of the graph. The aim of this question is to determine if some other symmetries are present.

   (a) [4] Does the McGee graph have an automorphism which maps some red vertex to a blue vertex? If your answer is yes, show the automorphism on the attached Question 5(a) worksheet. If you say no, justify your answer. Hint: consider the vertices at distance 4 from the root of the BFS tree from your answers from the previous question.

   (b) [4] Does the McGee graph have an automorphism which maps some red vertex to a green vertex? If your answer is yes, show the automorphism on the attached Question 5(b) worksheet. If you say no, justify your answer.

   (c) [4] Does the McGee graph have a symmetry which reverses the top 8-cycle? That is, the symmetry starts out like this:
   (0) (1 7) (2 6) (3 5) (4) ...
   If your answer is yes, show the automorphism on the attached Question 5(c) worksheet. If you say no, justify your answer.

   (d) [3] What is the automorphism group order of the McGee graph? Hint: the only types of symmetries it has are the types you have explored so far. Explain your answer in terms of what the symmetries do to the vertices of the graph.

6. Given a fixed root vertex v, the edges of the McGee graph can be divided into classes:
   1. The edges which are in the BFS tree of v that goes down to the vertices at distance at most 3 from v.
   2. Chords connecting pairs of vertices at distance 3 from v.
   3. Edges between one vertex at distance 3 from v and another one at distance 4.
   4. Edges between two vertices at distance 4.
   The number of edges in class 1 is the same for every vertex since the graph is a (3,7)-cage. The numbers in classes 3 and 4 are easy to see. From there you can get the number of chords. The 7-cycles which include vertex v are in one to one correspondence with these chords since every 7-cycle has a unique edge such that both of its endpoints are at distance 3 from v.

   (a) [1] Apply the hints above to count the number of 7-cycles containing one specific red vertex.

   (b) [1] Apply the hints above to count the number of 7-cycles containing one specific blue vertex.

   (c) [1] Apply the hints above to count the number of 7-cycles containing one specific green vertex.

   (d) [7] Use the information from parts (a), (b) and (c) to determine the number of 7-cycles in the McGee graph.

   ---

   A worksheet has been provided for your use for the next two questions. You should print this and use it for your answers.

7. (a) [10] Use the Edmonds/Karp maximum flow algorithm to find a maximum s,t-flow in the network N as pictured on the attached worksheet. This algorithm is the one which finds augmenting paths of the auxillary graph using BFS.

   (b) [3] Show the cut in the network obtained by letting P be the set of vertices reachable from s in the final auxillary graph of part (a).

   (c) [2] Show that there can be more than one maximum flow in a network by giving a maximum flow for N which is different from the one you found in part (a).

8. [10] Find a Gomery-Hu cut tree of the multi-graph pictured on your worksheet. Show your work on the worksheet as directed.