0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 1 1 1 0 0 0 1 0 0 0 0 0 0 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0
For our domination algorithms, a vertex is coloured red if it is in the dominating set, white if its status is undecided and blue if it is excluded from being included in the dominating set. We discussed several bounding strategies in class:
(i) Using the maximum degree DELTA from the original graph.
(ii) Using the domination degrees of the white vertices. The domination degree of a white vertex is the number of undominated vertices it can dominate.
(iii) Using the maximum dominator degrees for each of the undominated vertices. The maximum dominator degree for an undominated vertex v is equal to the maximum domination degree of a white vertex that dominates v.
For the next question, assume that the graphs under consideration have n vertices and maximum degree DELTA and they are stored in an adjacency list data structure as described for assignment #4. Assume that the number u of undominated vertices and the number w of white vertices are known. Give pseudocode that runs as fast as possible. Explain the data structures you will use and maintain. Give code both for computing the bound, and for maintaining any data structures you decide to use to reflect changes that occur when vertices change colour. Express your time complexities. as functions of w, DELTA and n. For assignment #4, we assumed DELTA was a constant but use DELTA instead of making that assumption for your analysis.
(b) [10] Analyze the steps your algorithm from (a) using Big Oh notation.
(a) [5] What lower bound do you get for the dominating set size using bounding strategy (i)?
(b) [5] What does the Sloane On-line Encyclopedia of integer sequences give as the size of a minimum dominating set?
(c) [10] Using just simple observations and algebra, what is the minimum size of a dominating set that has a row (corresponding to one 14-cycle in the second copy of C14) that has no dominating set vertices? Justify your answer.
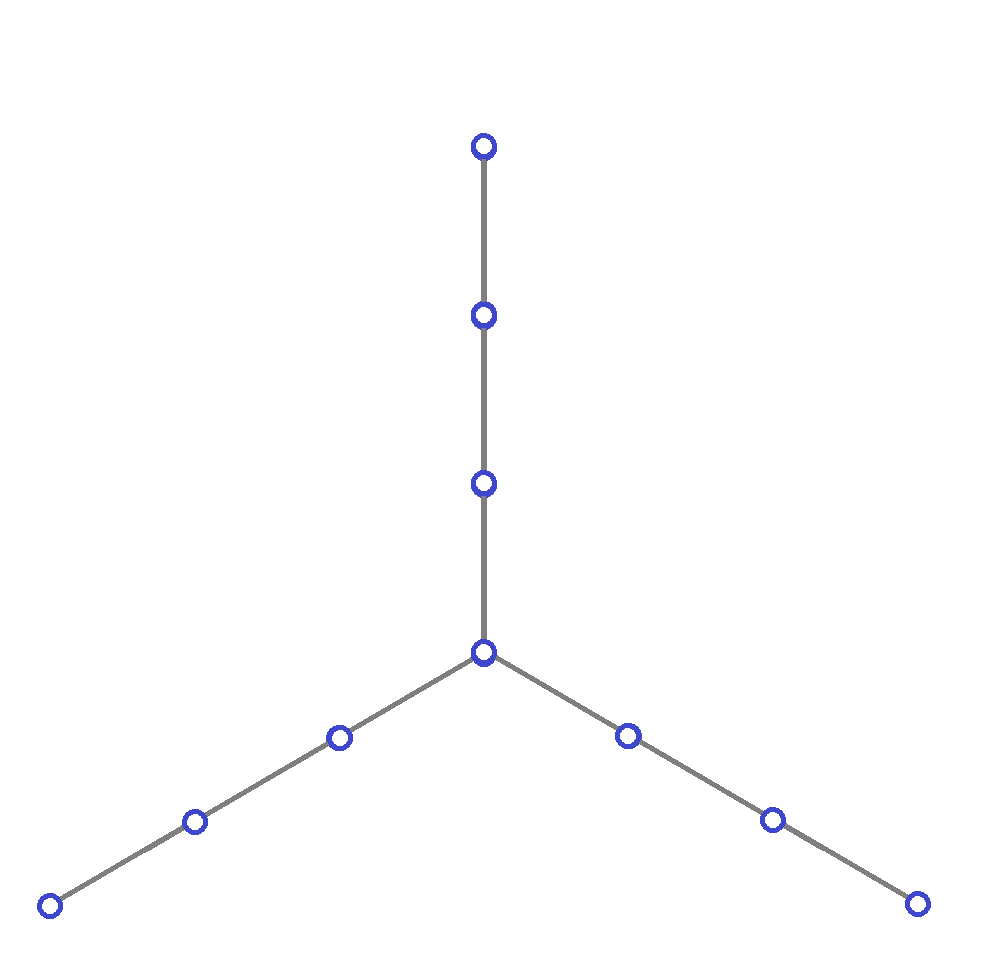
and a cycle on 10 vertices what values do the three bounds give at the start of the computation? Explain your computations.
If you take the Cartesian product of two 6-cycles the resulting graph is:
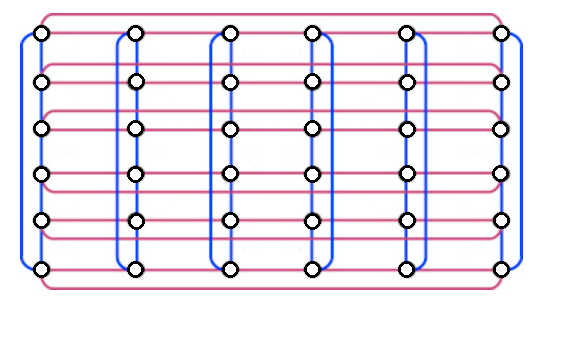
The Cartesian product of two 6-cycles has exactly one minimum dominating set up to isomorphism. If the lexicographic minimum set is chosen as the canonical form, the canonical dominating set is:
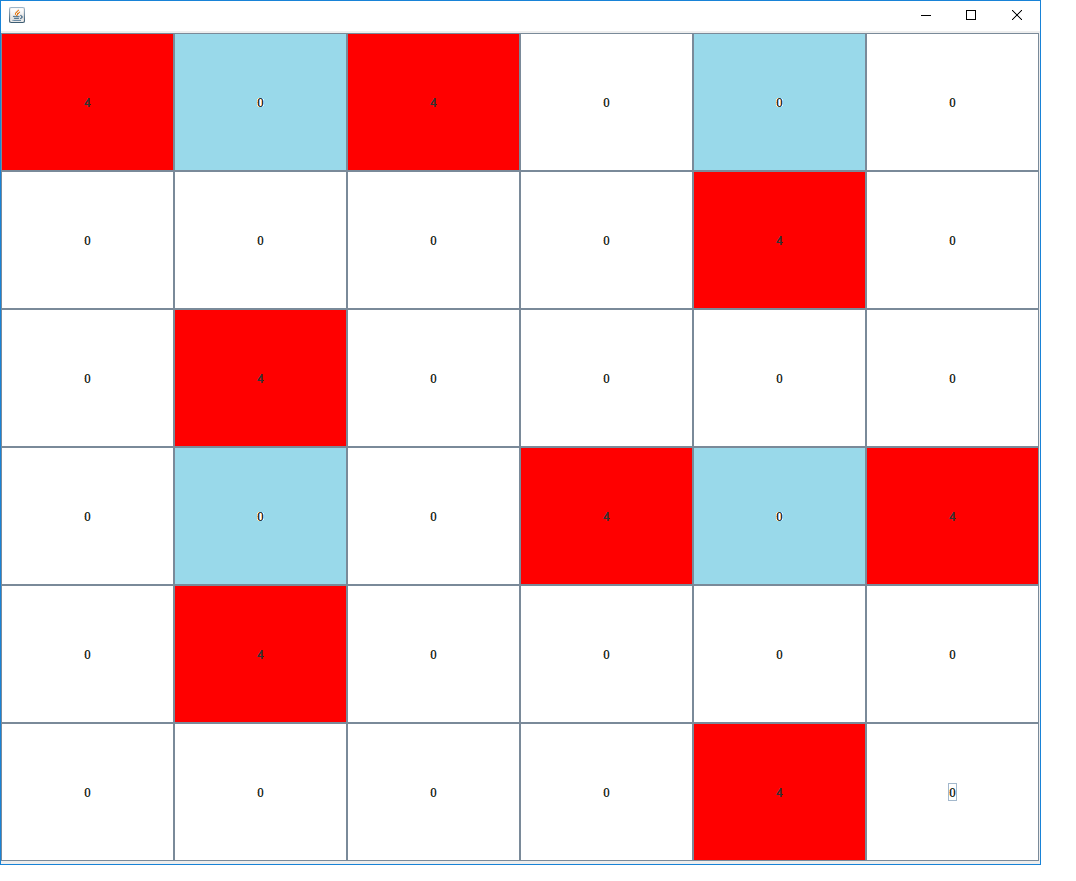
0 2 10 13 21 23 25 34If the vertices are numbered one row at a time from left to right, dominating set vertices are coloued red, and vertices dominated more than once are coloured blue, the dominating set looks like this:
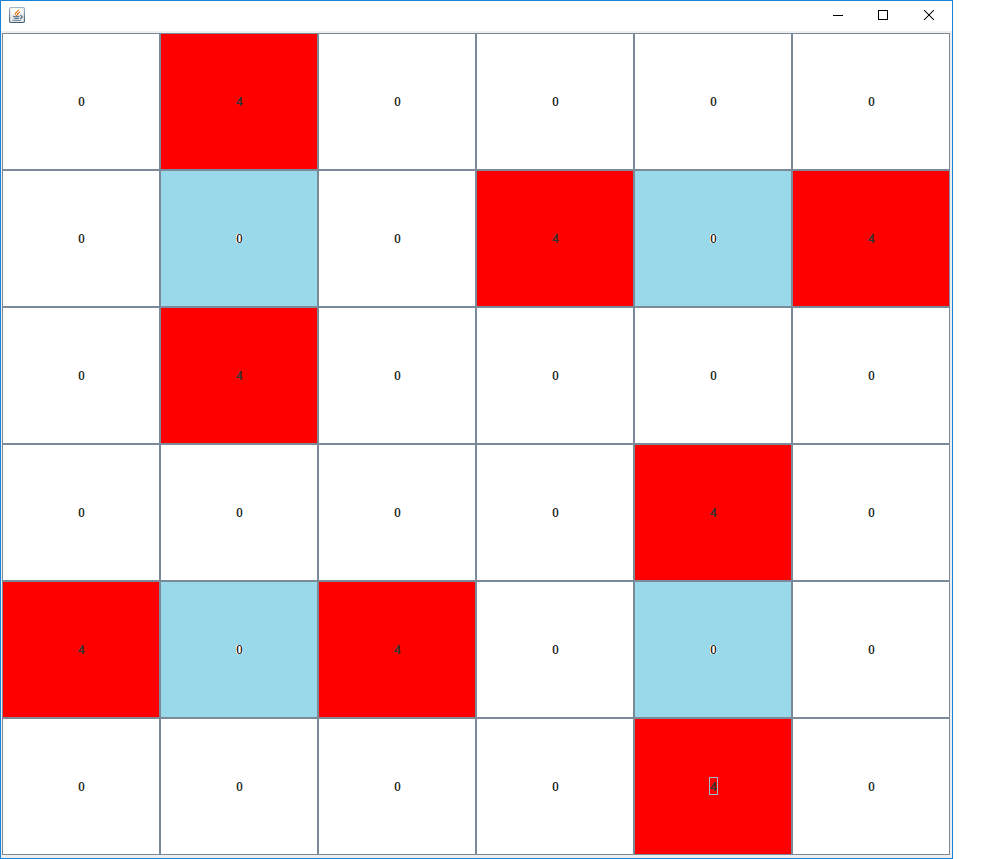
This picture shows an isomorphic dominating set but now the picture has a symmetry which is a 90 degree rotation:
Let n be the number of vertices. The input format is:
n group_order permutations in the group and then for each dominating set the dominating set size is given followed by the vertices in the dominating set.
For example, when k is 6, n= 6*6= 36 and the input starts with:
36 288 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 5 4 3 2 1 0 11 10 9 8 7 6 17 16 15 14 13 12 23 22 21 20 19 18 29 28 27 26 25 24 35 34 33 32 31 30The first line has n and the automorphism group order size. Lines 2-7 have the identity permutation. Line 8 is blank. Lines 9-14 have the symmetry created by reflecting over a vertical axis.
The last permutation is:
28 22 16 10 4 34 27 21 15 9 3 33 26 20 14 8 2 32 25 19 13 7 1 31 24 18 12 6 0 30 29 23 17 11 5 35
Then the file has 18 dominating sets of size 8:
8 5 8 12 16 20 29 31 33 8 5 7 9 17 20 24 28 32 8 4 7 15 17 19 28 30 32 8 4 6 8 16 19 27 29 31 8 3 7 11 15 18 26 28 30 8 3 6 14 16 18 27 31 35 8 3 5 7 16 18 20 28 31 8 2 11 13 15 23 26 30 34 8 2 6 10 14 23 25 27 35 8 2 4 6 15 19 23 27 30 8 1 10 12 14 22 25 33 35 8 1 9 11 13 22 24 26 34 8 1 5 9 12 20 22 24 33 8 1 3 11 14 18 22 26 35 8 0 9 13 17 21 24 32 34 8 0 8 10 12 21 25 29 33 8 0 4 8 17 19 21 29 32 8 0 2 10 13 21 23 25 34
You can see the whole file here:
When I run the program on this input file, the output I get is 18 lines that look like this:
16 8 0 2 10 13 21 23 25 34The 16 is the automorphism group order of the solution, the 8 indicates that there are 8 vertices in the dominating set and then the 8 vertices in the dominating set are listed.
(a) [5] Hand in the listing for your program.
(b) [25] Run your program on the input files for k=9 and k=11:
in_c09.txt (Right click here to download)
in_c11.txt (Right click here to download)
After you run your program use the system sort to get rid of duplicates to get one copy of each solution up to isomorphism. On linux I use:
sort -u < out.txt > sout.txt
Summarize the output you get on the attached worksheet When you indicate the dominating sets on the grid, colour the squares that correspond to dominating set vertices red. Colour the squares that correspond to vertices dominated more than once in blue. The program Cycles.java available in the connex resources can help in visualizing the dominating sets and shifting them so that you get an isomorphic solution.`