CSC 422/522: Assignment #1: Summer 2017
Due at the beginning of class on Friday May 19.

Instructions for all assignments:

1. Draw boxes for your marks on the top of the first page of your submission. Place a 0 in the corresponding box for any questions you omit. For this assignment:

   Question	1	2	3	4	5
   Marks	0	0	0	0	0

2. Questions should be in order.
3. Show your work unless otherwise stated.
4. Please put your name on your assignment.

1. A dominating set S of a graph G is a subset of the vertex set of G such that every vertex v of G is either in S or it has at least one neighbour in S.

   (a) [1 mark] How small can a minimum dominating set be for a connected graph on n vertices? Give an example of a graph on 8 vertices that realizes your bound.
   (b) [1 mark] How big can a minimum dominating set be for a graph on n vertices? Give an example of a graph on 8 vertices that realizes your bound.
   (c) [3 marks] How big can a minimum dominating set be for a connected graph on n vertices? Give an example of a graph on 8 vertices that realizes your bound.

   Given a connected n-vertex graph G, your answer to (a) is giving a lower bound on the size of its minimum dominating set and (c) gives an upper bound.

2. Consider the graph G:
   
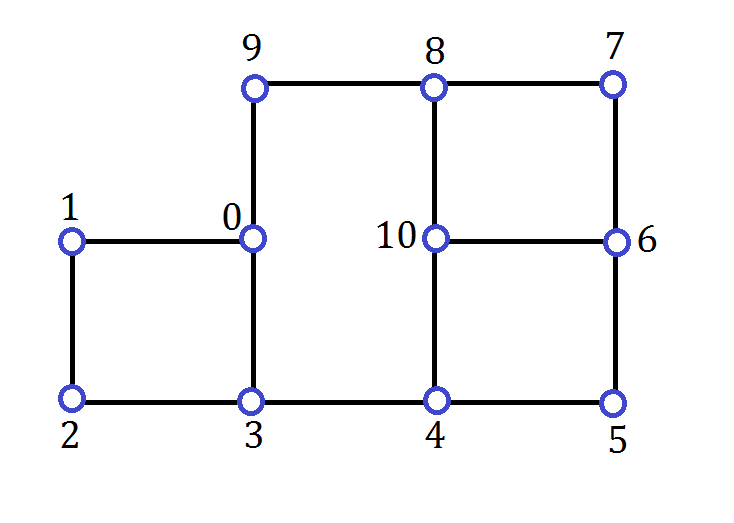
   (a) [1 mark] What is the degree sequence of G?
   (b) [1 mark] List the degrees in order from smallest to largest.
   (c) [2 marks] Give a tight lower bound B on the size of a minimum dominating set for a graph with this degree sequence.
   (d) [2 marks] Draw a graph with the same multi-set of degrees as G that has a dominating set of size B (from part (c)).
   (e) [2 marks] Give a minimum dominating set for G.
   (f) [7 marks] Prove that G has no dominating sets of size B (from part (c)).

   Hint: you probably have to do a case by case analysis for your proof. For example, maybe start by considering two cases:
   Case 1: Vertex 0 is in the dominating set.
   Case 2: Vertex 0 is not in the dominating set.
   The cases can have subcases that you should number systematically, for example Cases 1.1 and 1.2.

3. A k-prism is a 3-regular graph on 2k vertices that has two k-cycles, and edges connecting the ith vertex on the first k-cycle to the ith vertex on the second k-cycle. Number the vertices of a k-prism so that one cycle is labelled with with 0, 1, 2, ... , k-1, and the other cycle is labelled with k, k+1, ..., 2k-1. The remaining edges connect vertex i to vertex i+k for i = 0 to k-1.
   (a) [5 marks] Find a minimum dominating set for the k-prism for k=3, 4, 5, 6 and show your answers on the attached Prism Worksheet
   (b) [5 marks] Give a formula for the minimum dominating set order of a k-prism in terms of the number of vertices that it has. Hint: your formula should consider four cases: n/2 is congruent to 0, 1, 2, or 3 modulo 4.
   [Definition: For integers, n, r, and k, n is conguent to r modulo k if n= ck + r for some integer c.]
   (c) [10 marks] For each case from (b), argue that it is not possible to find a smaller dominating set.
   

   ---

   For questions #4 and #5, the algorithms presented operate by assigning colors to the vertices of a graph. Initially all vertices are white (undecided). Red vertices are in the dominating set, and blue ones are excluded. The dominating set D returned by the algorithm is the set of red vertices.

4. [10 marks] One iteration of Algorithm #1 (Random Vertex Order Greedy) behaves as follows. A random permutation p of 0 to n-1 is generated. Then for i from 0 to n-1, vertex p[i] is colored blue as long as the resulting colored graph has no blue vertices with all blue neighbours. Otherwise, p[i] is colored red.

   Given a graph G and a minimum dominating set D, does there always exist some permutation p so that Algorithm #1 returns D? If you answer "yes", then explain how to compute such a permutation p from the dominating set D. If your answer is "no", give a counterexample consisting of a graph G and a minimum dominating set D, and show that there is no permutation of the vertices for which the algorithm returns D.

5. [10 marks] One iteration of Algorithm #2 (Random BFS order greedy) A random root vertex r is selected. BFS is performed on the graph starting with vertex r. When the neighbours of a vertex are traversed, they are traversed in random order. The queue for the BFS contains a permutation p of the vertices that we will call a BFS-ordering. Algorithm #2 then proceeds as per Algorithm #1 using the BFS-ordering p.

   Given a graph G and a minimum dominating set D, does there always exist some BFS-ordering p so that Algorithm #1 returns D? If you answer "yes", then explain how to compute such a BFS-ordering p from the dominating set D. If your answer is "no", give a counterexample consisting of a graph G and a minimum dominating set D, and show that there is no BFS-ordering of the vertices for which the algorithm returns D.