CSC 422/522: Summer 2017 Assignment #2
Due at the beginning of class, Friday June 2

Instructions for all assignments:

1. Draw boxes for your marks on the top of the first page of your submission. Place a 0 in the corresponding box for any questions you omit. For this assignment:

   Question	1	2	3	4	5	6	7	8	9	10
   Marks	0	0	0	0	0	0	0	0	0	0

2. Questions must be submitted in order.

1. For this question consider this graph:

   

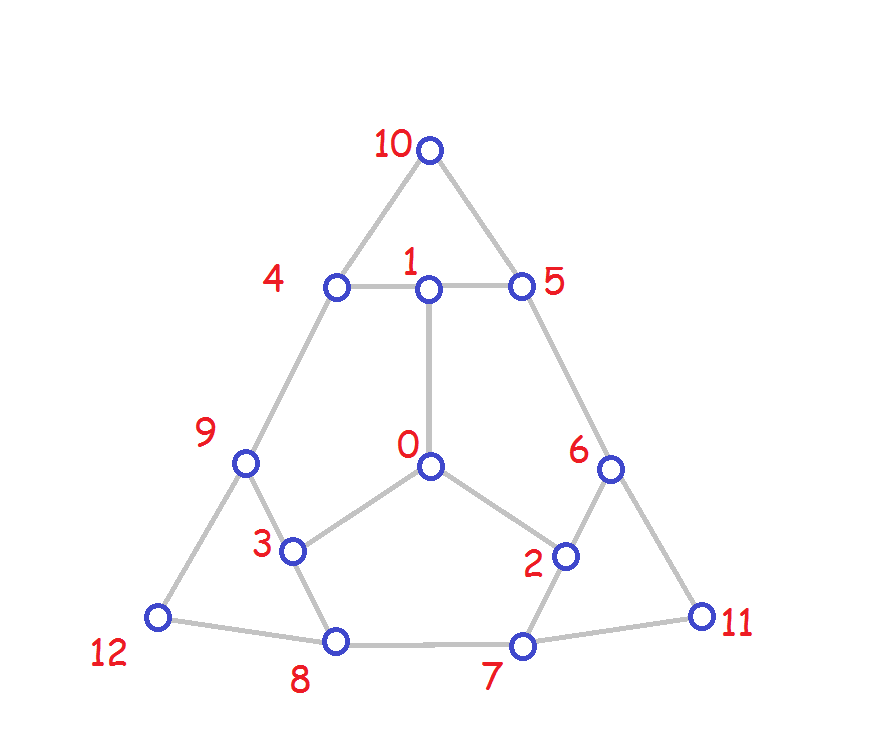
   (a) [3] List all the automorphisms of this graph in lexicographic order using one line notation.
   (b) [4] Give the cycle structure notation for each of the automorphisms from (a).
   For the dominating sets for part (c) and (d) show the relabelled dominating sets corresponding to each automorphism and give the:

   1. Number of automorphisms mapping the dominating set to itself.
   2. Number of different equivalent dominating sets.
   3. Lexicographic minimum representative of the dominating set.

   (c) [4] The dominating set is:

   

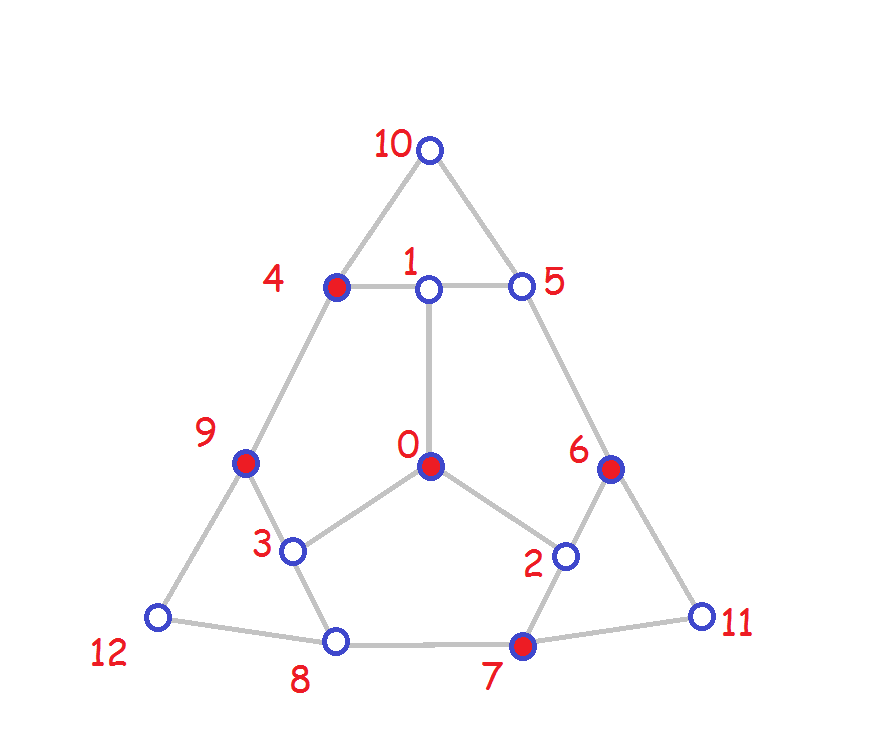
   Click here for a worksheet for part (c).

   (d) [4] The dominating set is:

   

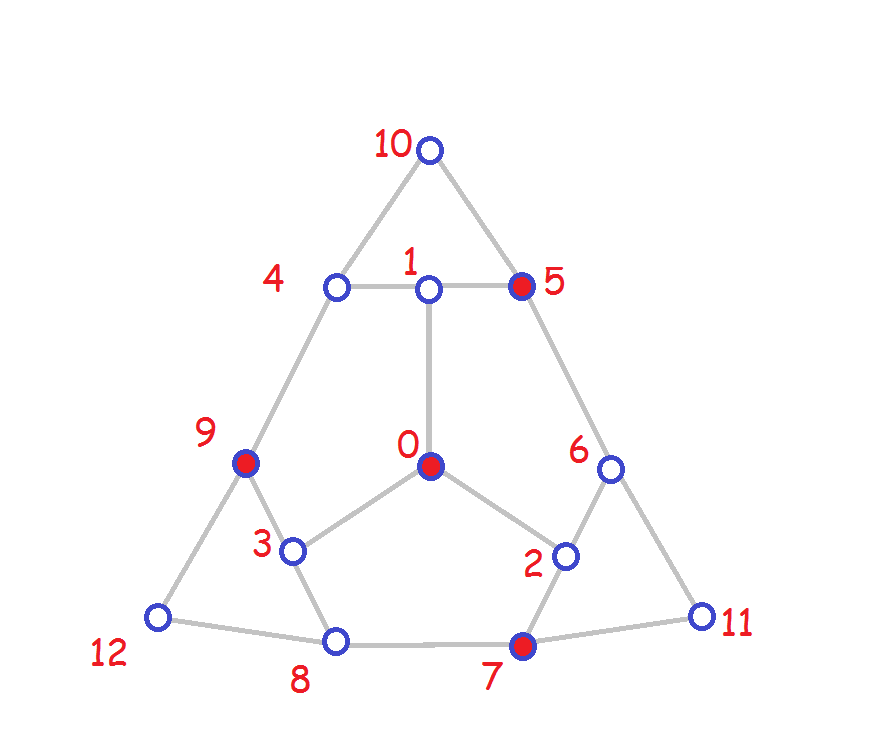
   Click here for a worksheet for part (d).

2. [10] Compute the ()-canonical form for this tree showing your work at each step.

   

3. [5] A star is a tree such that every vertex except one is a leaf (a leaf is a vertex of degree one). The sets of strings of parentheses for stars can be described as the set of strings of the form ( [ ( ) ]^k ) where k is the number of leaves of the star.
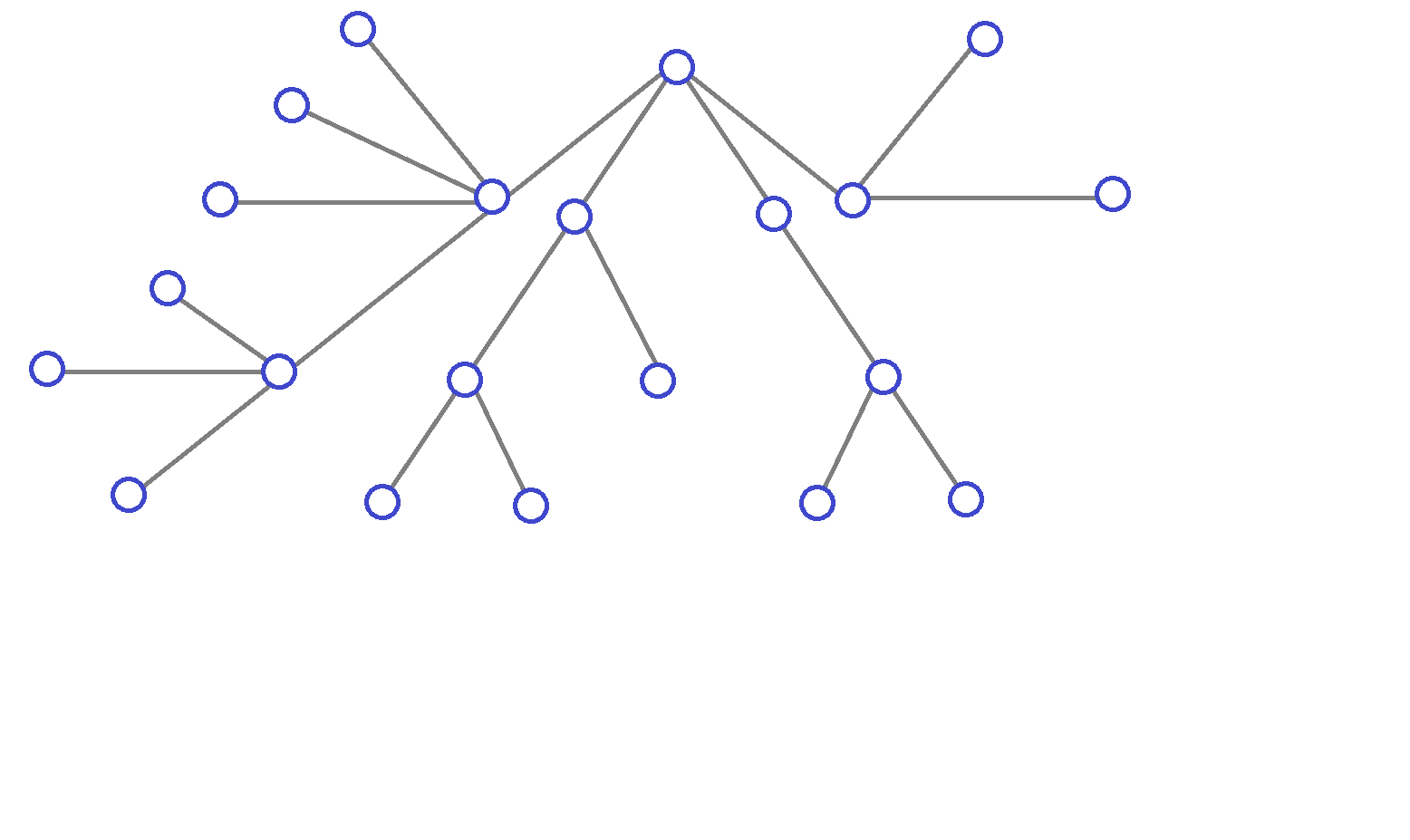
   Describe the set of strings of parentheses which are the canonical forms for the paths (tree such that two vertices have degree one and the remaining vertices have degree two).

4. (a) [3] Draw one representative for each isomorpism class of a tree on n vertices for n from 1 to 7. List the trees systematically with those having larger diameter listed before the ones with a smaller diamater.

   (b) [3] For each tree from (a), color the vertices of a minimum dominating set of the tree.

   (c) [3] Make a conjecture (for n at least 2) for a formula for the maximum size of a minimum dominating set for a tree on n vertices and give examples to show that there are trees meeting this bound for each value of n at least 2.

   (d) [6] Prove by induction that a tree has dominating set order at most the value given by your bound. Try using strong induction (you assume the formula is correct for n=2, 3, ..., n) in order to prove it is true for n+1. If you are using strong induction, you can remove more than one vertex from the tree at one step.

   For questions 5-7 below, you can print as many copies as you need of these worksheets. Use the first two for doing clockwise-BFS in directions clockwise or counterclockwise. The unlabelled picture can be used for showing the non-equivalent labelled embeddings.

   1. Labelled K_3,3.
   2. Flip of K_3,3.
   3. Unlabelled picture of K_3,3
   Be sure to indicate on each copy the number of the question you are answering.

5. Consider this labelled embedding:

   

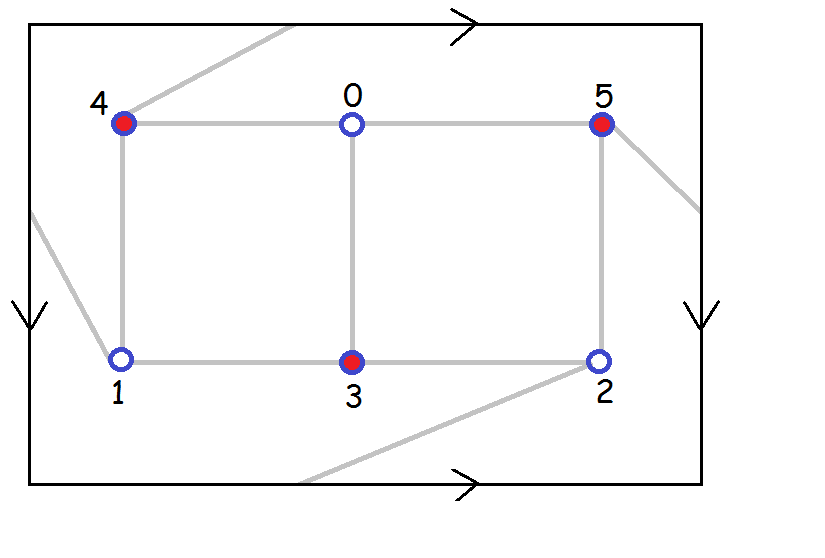
   (a) [3] Write down a permutation (in one line format) for each automorphism of the embedding. How many automorphisms are there?
   (b) [2] For this embedding and its automorphisms, what are the orbits for the vertices? Two vertices u and v are in the same orbit for this embedding if there is an automorphism of the embedding that maps u to v.

6. (a) [4] For each choice of orbit choose one vertex r, and then for each choice for selecting a first child f to be one of the three neighbours of r, show the resulting labelled embedding that arises from applying clockwise-BFS with root r, first child f, and the direction clockwise, and then from applying clockwise-BFS with root r, first child f, and the direction counterclockwise,

   (b) [4] Write down the resulting adjacency lists from (a).

   (c) [3] Which of these adjacency lists is the lexicographic minimum?

   (d) [4] Argue in terms of the embedding symmetries why it is that we do not have to consider other choices for r, f in order to ensure the lexicographic minimum has been found.

7. [5] Indicate the choices for root r, first child f, and direction d that correspond to labellings of the embedding which have the same rotation system as the lexicographic minimum [determined in the previous question]. For each one, finish labelling using the clockwise-BFS. Hint: the number of these should equal the number of automorphisms of the embedding.

8. Consider the graph K_3,3, labelled so that vertices 0, 1, and 2 are non-adjacent and vertices 3, 4, and 5 are non-adjacent. The adjacency matrix of K_3,3 with this labelling is:

   0	0	0	1	1	1
   0	0	0	1	1	1
   0	0	0	1	1	1
   1	1	1	0	0	0
   1	1	1	0	0	0
   1	1	1	0	0	0

   

   
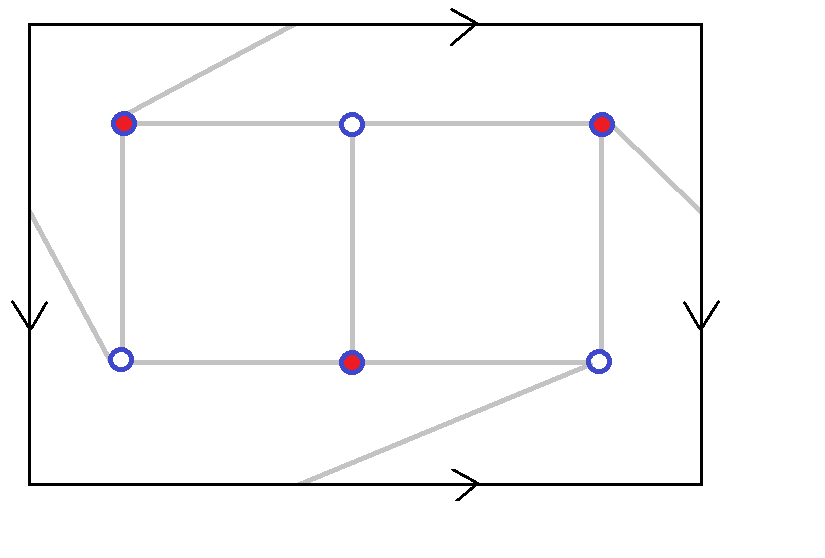
   (a) [2] How many ways can you label the pictured embedding (not worrying about symmetry-equivalence) so that the adjacency matrix of the resulting graph is the one given above for K_3,3. Hint: make sure {0,1,2} is an independent set and that {3,4,5} is an independent set. Explain your reasoning for this question.
   (b) [2] Compute the number of non-equivalent embeddings of K_3,3 that look like the one pictured: it will be your answer from (a) divided by the order of the automorphism group for the embedding.
   (c) [6] Show each of the different non-equivalent labellings [that you counted in part (b)] of the embedding of K_3,3.

9. Consider this rotation system:
   

   0: 1 3 5 4
   1: 0 4 6
   2: 3 4 5
   3: 0 6 4 2
   4: 0 5 2 3 6 1
   5: 0 6 2 4
   6: 1 4 3 5
   

   (a) [4] Use the face walking algorithm described in class to walk all the faces of this embedding.

   (b) [2] What is the genus of the embedding and what surface does this correspond to?

   (c) [4] Draw a nice picture of this embedding.

10. Consider this rotation system:
    

    0: 1 3 5
    1: 0 4 2
    2: 1 3 5
    3: 0 4 2
    4: 1 3 5
    5: 0 4 2
    

    (a) [3] Use the face walking algorithm described in class to walk all the faces of this embedding.

    (b) [1] What is the genus of the embedding and what surface does this correspond to?

    (c) [2] Draw a nice picture of this embedding.

    (d) [2] Is this graph isomorphic to the graph from question 5? If the answer is yes, provide an isomorphism. If the answer is no, justify your answer.

    (e) [2] Is this embedding isomorphic to the embedding from question 5? If the answer is yes, provide an isomorphism. If the answer is no, justify your answer.