CSC 425/520: Assignment #4: Fall 2016
Due at the beginning of class on Friday Dec. 2.

Instructions for all assignments:

1. Draw boxes for your marks on the top of the first page of your submission. Place a 0 in the corresponding box for any questions you omit. For this assignment:

   Question	1	2	3	4	5	6	7	8	9
   Marks	0	0	0	0	0	0	0	0	0

2. Questions should be in order.
3. Show your work unless otherwise stated.
4. Please put your name on your assignment.

1. [12] Use the Edmonds/Karp maximum flow algorithm to find a maximum s,t-flow in the network N as pictured on the attached worksheet.

2. [4] Show the cut in the network obtained by letting P be the set of vertices reachable from s in the final auxillary graph for Question #1.

3. [4] Show that there can be more than one maximum flow in a network by giving a maximum flow for N which is different from the one you found for Question #1.

4. Consider the following graph G:

   

   
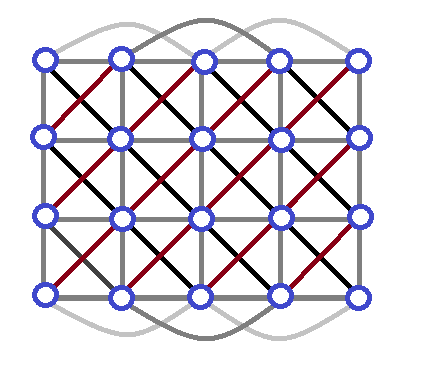
   (a) [5] Color the vertices of this graph using the greedy coloring algorithm. Process the vertices one row at a time going from top to bottom. For a given row, process the vertices going from left to right. For your color choices, use these colors in the order given: red, blue, green, orange, yellow, purple. If you do not have colored pens or markers, you can either use paint or write r, b, g, o, y, p beside the node to indicate the color.

   (b) [5] Use the colorful clique algorithm to determine if G has a clique of size 5 or not. The first step is the coloring you did for part (a). Explain each step that the algorithm takes from that point onwards.

5. In the Keller graph of dimension k, the vertices correspond to k-tuples that use the symbols 0, 1, 2, and 3. Two vertices are adjacent if their tuples differ in two or more positions, and there is at least one position where the difference is 2 modulo 4. These tuples are in a 5-clique for the Keller graphs of dimension 3:

    0 0 0 
    0 1 2 
    1 2 0 
    2 0 3 
    2 2 2
   

   
   (a) [5] Apply the doubling construction presented in class to construct a 10-clique in the Keller graph of dimension 4.
   (b) [5] A maximal clique S in a graph has the property that for any vertex u of G that is not in S, S union {u} is not a clique. Is the clique you found for part (a) a maximal clique in the Keller graph of dimension 4? Justify your answer.

6. The Petersen graph:

   

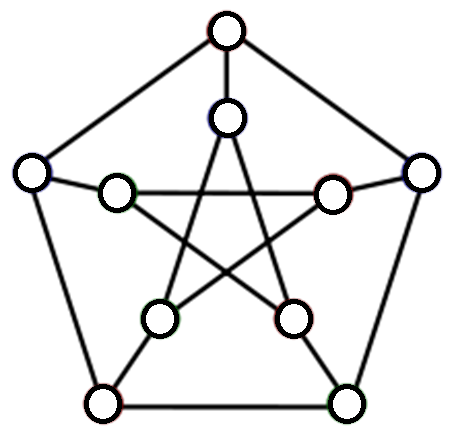
   (a) [5] Analogous to what I did for the 120-cell, set up a linear programming problem for an upper bound for the maximum independent set order of a Petersen graph.

   The variables you should use (in this order) are: R, P0, P1, P2, B0, B1, B2, B3. The equations should state that:

   • The number of vertices is 10.
   • The number of pentagons is the total number that the Petersen graph has. Hint: the graph is vertex-symmetric so each vertex is in the same number of pentagons.
   • The number of reds matches up with the numbers you find in the pentagons.
   • The number of reds matches up with the numbers you find as neighbours of the blue vertices.
   
   (b) [5] An optimal solution to this problem has R=4, P0=0, P1= 0, P2=12, B0=0, B1=0, B2=6, B3=0. Show an independent set of the Petersen graph that realizes the values obtained for this optimal solution or explain why no such independent set can exist.

7. This question is about 2-trees that are fans or ladders.
   

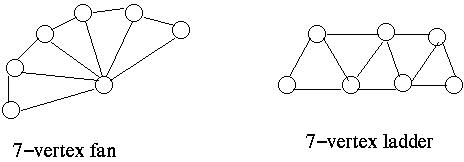
   (a) [5] Compute the number of spanning trees on the fans which have with 3, 4, 5, and 6 vertices using the algorithm for 2-trees presented in class.
   (b) [5] Prove that an n-vertex fan has the same number of spanning trees as an n-vertex ladder using the series-parallel algorithm for counting spanning trees presented in class.

8. Consider the following graph:

   

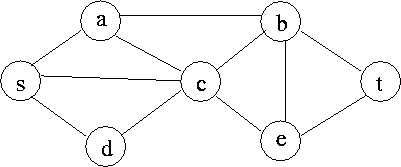
   (a) [10] Show the directed graph you would use if your aim was to compute the minimum number of vertices in an s,t-vertex cut.
   (b) [5] Apply the Edmonds-Karp flow algorithm to this network. You do not have to show your work. Indicate the final network flow.
   (c) [5] Show the cut in the network obtained by letting P be the set of vertices reachable from s in the final auxillary graph for this question. Which vertex cut from the original graph does this correspond to?

9. [20] Fill in the attached worksheet (ham_path.pdf) for Hamilton Paths of 2-trees.