Final Project
CSC 422/522, Fall 2014
Dominating Set Challenge- Exact Algorithm

Due date: Tues. Dec. 9 by 11:55pm.
Late deadline: Tues. Dec. 16 at 11:55pm with a 10% late penalty.

The goal is to design a fast C or C++ program for the dominating set problem. The program takes as input a sequence of graphs, and finds a minumum dominating set for each one.

Input must be from standard input. and output must go to standard output. I am going to run it like this:
a.out < in.txt > out.txt

Do not hardcode a file name into your program. Your programs will be tested for correctness using various command files. If you want your program to run correctly, it is very important to follow the input and output specifications exactly.

Use:
#include <stdio.h>
#include <stdlib.h>
Some compilers include these automatically. Others do not and programs without them do not compile.

Use a constant NMAX for the maximum number of vertices:
#define NMAX 800
If you use an adjacency list data structure, you can use:
#define MAX_DEGREE 200 // Modified for next time.
If NMAX is not big enough, print an error message that explains that the user should increase NMAX and recompile. If MAX_DEGREE is not big enough, print an error message that explains that the user should increase MAX_DEGREE and recompile. Do not use malloc/free. Using repeated malloc/free calls will end up slowing the program down and could create bugs that cause memory leaks. Memory leaks are a disaster when you are working with large computations.

The Input Format

Vertices of an n-vertex graph are numbered from 0 to n-1.
A graph is input as:
<number of vertices>
Then for each vertex v:
<degree of v> <neighbours of v>

Your program should permit the user to use arbitrary amount of white space and arbitrary line spacing when typing these numbers in.

For example, an input file like this:

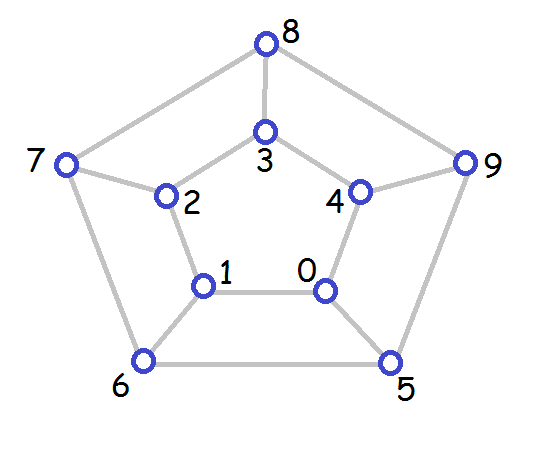
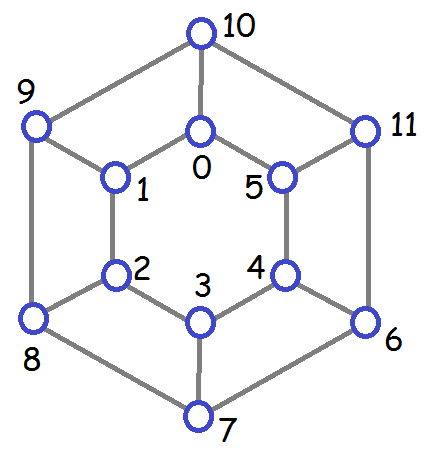
 10
3   1   4   5
3   2   0   6
3   3   1   7
3   4   2   8
3   0   3   9
3   0   9   6
3   1   5   7
3   2   6   8
3   3   7   9
3   4   8   5

 12
3   1   5   6
3   2   0   7
3   3   1   8
3   4   2   9
3   5   3  10
3   0   4  11
3   0  11   7
3   1   6   8
3   2   7   9
3   3   8  10
3   4   9  11
3   5  10   6

Represents the following two graphs:

The Output

For each graph, first print the graph number (number the graphs starting at 1) followed by the number of vertices. Each time you find a better dominating set, print it. To print a dominating set:
First print either 0 or 1 where:
0 means that the dominating set is the best found so far, and
1 means that the dominating set is a minimum dominating set for the graph.
Then print the number of vertices in the dominating set followed by the vertices in the dominating set. It is assumed that after you have printed a dominating set prefaced by 1 that the computation on that graph has completed.

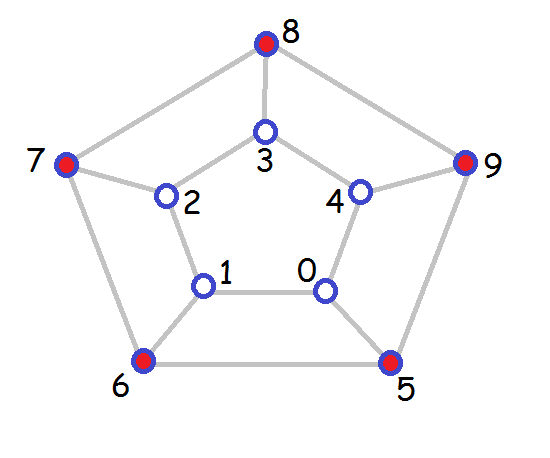
For example, for the input file above, the output might be:

  1  10
0   5   5   6   7   8   9 
0   3   4   6   7 
1   3   4   6   7 

  2  12
0   6   6   7   8   9  10  11 
0   4   5   7   8   9 
1   4   5   7   8   9 

The second line represents this dominating set:

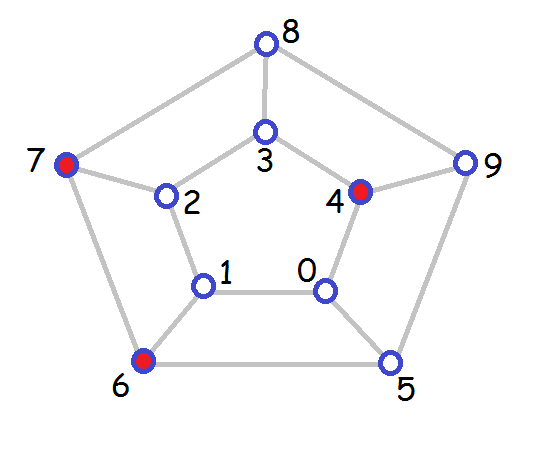
The third line is printed at the end of the computation for the graph and indicates that this dominating set is a minimum one.

The first line for the second graph represents this dominating set:

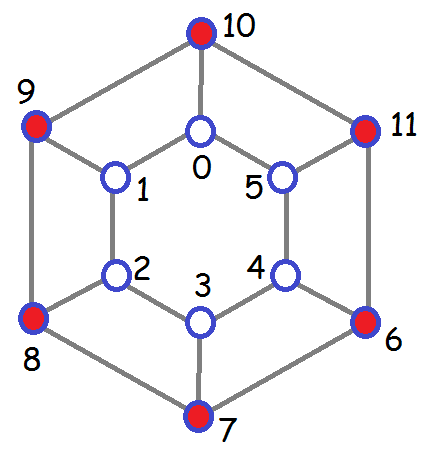
The second line gives this dominating set:

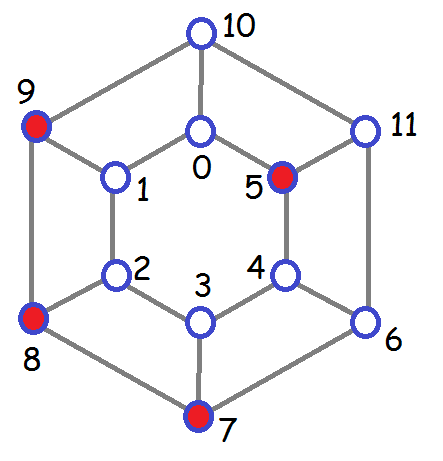
The third line for this graph indicates that this dominating set is a minimum dominating set.

IMPORTANT: The test cases could include problems that are too difficult for your program to solve in a reasonable amount of time. To get credit for what your program can do within the time limit, use
fflush(stdout);
each time you print a dominating set. Here is some sample code that you could use:

#include 
// Status 0 means the dominating set is the best so far.
// Status 1 means the dominating set is a minimum dominating set.
// Code created by Wendy Myrvold.
void print_solution(int status, int size, int dom_set[])
{
    int i;
    printf("%1d %3d ", status, size);
    for (i=0; i < size; i++)
        printf(" %3d", dom_set[i]);
    printf("\n");
    fflush(stdout);
}

Upload to connex:

Upload each file separately. Do not archive or compress the files. You are allowed an unlimited number of submissions until the deadline. Do not upload "draft" submissions (they do not get downloaded for marking).

1. For your program, preface each file name with your first name. For example, I might have:
   wendy_include.h
   wendy_io.c
   wendy_main.c
   Your program should compile if I use
   gcc *.c
   for a C program, or
   g++ *.cpp
   for a C++ program.
2. A .pdf document that describes the algorithm you implemented. Preface the file name with your first name. For example, I would use the file name wendy.pdf

Marking Scheme

For CSC 422 students, the exact algorithm is worth 30% of the final mark in the class, and designing a good heuristic algorithm merits bonus marks. For CSC 522 students, the exact algorithm is worth 20% of the final mark, and designing a good heuristic algorithm is worth 10%.

The marking scheme:

1. [5] Modular program design.
2. [5] Meaningful variable names.
3. [5] Lots of comments.
4. [5] Efficient application of chosen data structures.
5. [10] Creativity: addition of algorithm enhancements that improve the functionality of the basic algorithm presented in class.
6. [40] Correctness.
7. [10] Speed of execution. Note: a fast program that gives incorrect answers will not be rewarded marks for speed. Bonus marks will be rewarded for code that is substantially faster than the norm.
8. [20] Paper describing algorithm.